5.3机-光杠杆式测微放大机构

机-光杠杆是把测杆的位移量通过一定形式的机械杠杆的传递，变换为反射光线的偏转量，从而使被测微动量放大显示的一种机构。

图5-14所示机构是利用“正弦-正弦”型杠杆1和具有反射镜2的“正切_-圆弧”型机-光杠杆组成的放大系统。

当测杆微动量为y时，经杠杆1放大为Y′，然后通过中间传动杆3向机-光杠杆传递使反射镜2摆转β角。于是反射光线转移了2β角，从而获得与y相对应的放大量Y。按几何关系求得机构的放大倍数为

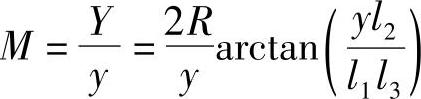
由上式可知，放大倍数是随y的变化而变化的。因此从理论上来讲，刻度盘是不能按线性关系刻制的。但在实际应用中，y在很小的范围内变化，机-光杠杆的摆转角β也很小，可近似地看作“圆弧-圆弧”式放大。所以放大倍数也可看作常数。

如果把中间传动杆3与反射镜2的安装架设计成如图5-4c所示的齿条与齿轮啮合形式。那么，此机-光杠杆部分则变成“圆弧-圆弧”型的对应式。于是整个机构的放大倍数就是常数，即η=1。这时，假定齿轮的节圆半径为l₃，则放大倍数M为

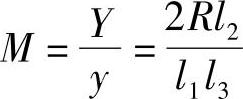
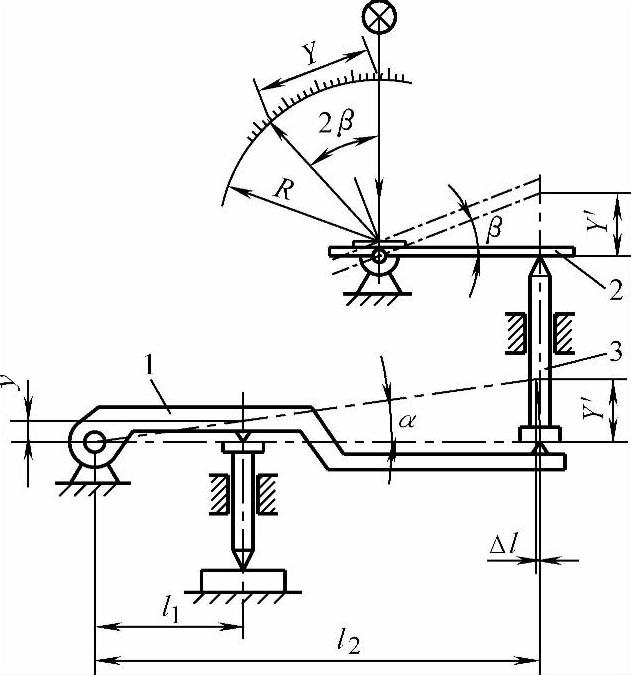
图5-14 机-光杠杆式测微放大机构

1—杠杆 2—反射镜 3—中间传动杆

(www.xing528.com)

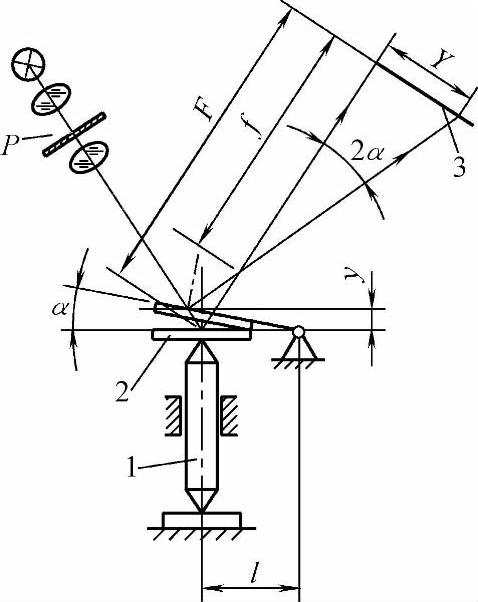
图5-15 “正切-正切”型机-光杠杆测微放大机构

1—测杆 2—反射镜 3—显示屏

图5-15所示是“正切-正切”型机-光杠杆式放大机构。通过针孔P的光线变为平行光线后投射到反射镜2上，并反射到显示屏3上形成针孔像。当反射镜2随测杆1的微量移动y而摆动α角时，由几何证明，反射光线则以2α角放大射到显示屏上，从而产生针孔像的移动量Y。F为反射镜与测杆的起始接触点A至显示屏3的距离，在测微机构中，α变化很小，f≈F，所以其放大倍数计算如下：

由几何关系，有y=ltanα

Y=ftan2α≈Ftan2α

所以放大倍数为

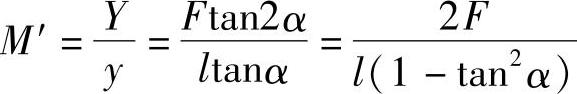
由上式可知，放大倍数不是常数。但当α在很小范围内变化时，可近似地看作为常数，即

M=2f／l

此种机构原理在光学比较仪、光学指示器、粗糙度测定仪和自动准直仪中均有应用。