如何合理确定转值和比例尺？

1）转值。转值就是调节机构指示器上指针每转一周或刻度盘一圈所代表的物理量。通常以A表示。如一个刻度盘等分为100个分划，每一分划代表1m，则其转值为A=100m／r。

若已知某一机件（指针、刻度盘或手轮）的转值为A，转数为n，则它所复现的物理量x为x=An。

转值的单位可根据被调对象而定。对于距离测量，单位是km／r、m／r、mm／r等；对于力的调节，单位是N／r；对于电感调节，单位是H／r或mH／r等。

2）比例尺。比例尺是指单位长度或单位转角所代表的物理量，以M表示。所以比例尺又分线位移比例尺（记为M_l）和角位移比例尺（记为M_α）。

若调节器或指示器的比例尺（M_l或M_α）及其实际位移量（直线L或转角φ）已知，则它所复现的物理量x为x=M_lL或x=M_αφ。

比例尺的单位也是根据研究对象而定的，如km／rad、m／mm或N／rad等。

3）转值与比例尺的关系。若调节机构的调节器和指示器两者中之一是作线位移计量的，则它们的转值与比例尺的关系为A=M_lL／n；若两者均作角位移计量，则它们的转值与比例尺的关系为A=M_αφ／n或A=360M_α（n=φ／2π）。就调节器或指示器本身而言，它的转值与其角位移比例尺的关系亦为A=2πM_α。

4）传动比与转值和比例尺的关系。引入转值和比例尺概念的目的，是在设计调节机构传动链时，便于进行运动学分析。因为传动链的传动比与转值和比例尺有密切的关系。

现在以图4-2所示的调节机构导出转值与传动比的关系。假定齿轮1、2的转值分别为A₁和A₂。当齿轮1转n₁转时，齿轮2有确定的转数n₂。因为它们所反映的物理量相等，所以有

A₁n₁=A₂n₂

根据传动比定义则有

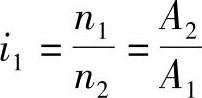
可见，调节机构的传动比等于从动轮转值与主动轮转值之比。根据转值所确定的传动比，则可确定齿轮的齿数。

同理可求得具有多种转值和多级传动的调节机构的传动比。图4-3所示是具有快速粗调和慢速细调的检测系统的调节机构。手轮1和2分别有不同的输入转值A₁和A₂（A₁＞A₂），通过蜗轮副z₅／k（k是蜗杆头数），由输出轴传至指示器，该输出轴有共同的预定转值A₀。

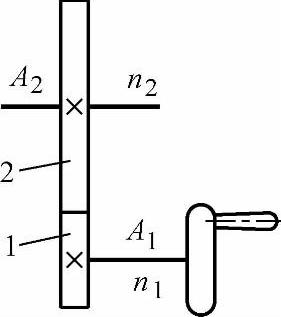
图4-2 转值与传动比关系

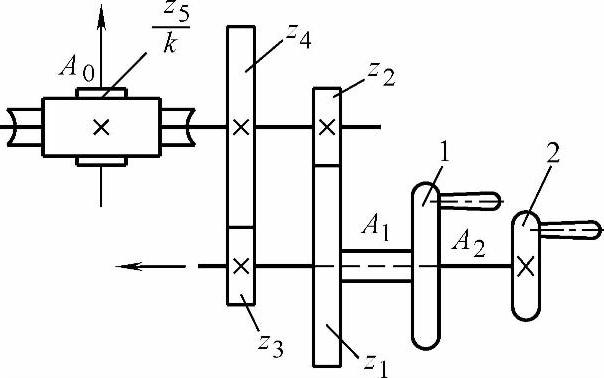
图4-3 有两个输入转值的调节机构

当需要快速调至目标值时，用手轮1以大转值A₁进行调节。这时调节机构传动链的传动比为

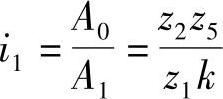
当接近目标值时，马上进入精确细调，这时需要以小转值A₂操纵手轮2。传动链的传动比则为

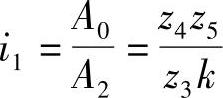
确定手轮大转值的条件是使调至目标值所需的时间尽可能最短。而确定手轮小转值的条件则是使精调误差最小。

5）转值计算举例。把调节器（旋钮或手轮）的旋转运动转换为指示器（指针）的直线位移运动的调节机构也是常用的，如频率调节机构、测量显微镜纵向测微机构和阀门调节机构等。下面举两例说明此类调节机构的转值计算。

［例4-1］图4-4所示为简单测距仪的调节机构。假设其测量范围为0～15000m，测量精度要求为±5m，螺杆1与螺母2之间存在回差为±0.05mm。试计算螺杆的有效长度和螺杆的转值。(www.xing528.com)

根据精度要求，刻度尺的比例尺应为

M=5m／0.05mm=100m／mm

于是得螺杆的有效长度为

l=15000m／100m／mm=150mm

若选择螺杆的螺距为5mm，则螺杆每转一转时，与螺母固连的指针3移动5mm。所以螺杆的转值为

A=100m／mm×5mm／r=500m／r

［例4-2］图4-5所示是光学测距仪补偿调节机构。传动链是由两个齿数为z₁和z₂的齿轮、螺距为P的螺杆2与螺母3，以及臂长为l₁和l₂的杠杆4组成。假定透镜5移动1mm相当于手轮上的刻度转过n个分划，试求手轮1的转值。

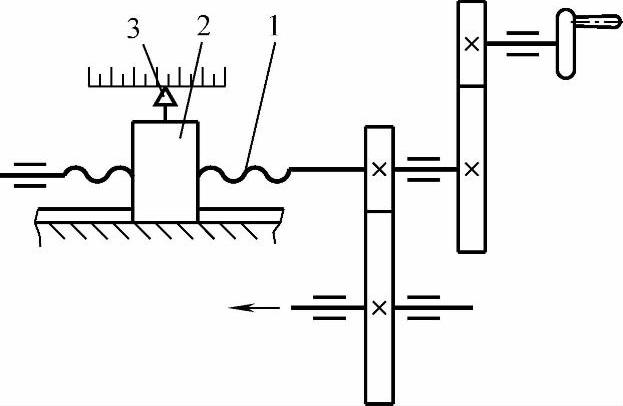
图4-4 旋转运动变直线位移的调节机构

1—螺杆 2—螺母 3—指针

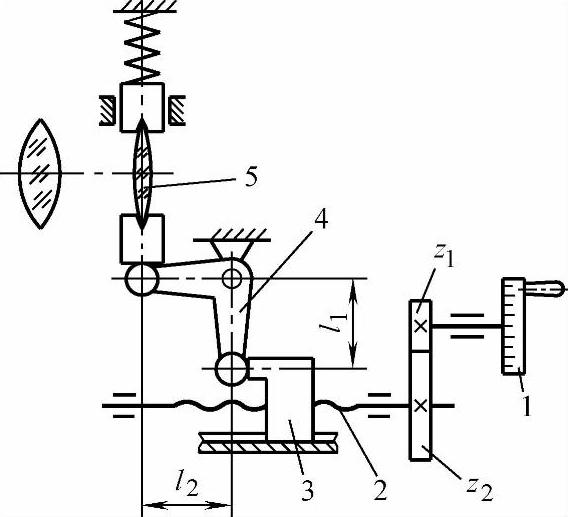
图4-5 由齿轮、螺杆和杠杆组合的调节机构

1—手轮 2—螺杆 3—螺母 4—杠杆 5—透镜

手轮转一周引起透镜5的位移量为

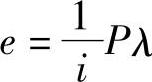
式中 i——齿轮副传动比；

P——螺杆螺距（mm）；

λ——杠杆的臂长比，λ=l₂／l₁。

所以手轮的转值为

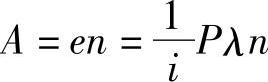
手轮转值的设计要注意两点：

1）在一定调节范围内，若手轮的转值大，则要调到某个测量值时，手轮转动的范围小（或转数少），所需的调节时间短，但调节精度低；若手轮的转值小，则要调到同样的测量值时，手轮转动的范围大（或转数多），所需的调节时间长，但调节精度高，容易控制。因此要根据使用场合和要求进行合理的转值设计。若要在短时间内粗调到某个较大的测量值，则要设计大转值的手轮；反之，若要得到精确的测量值，则要尽量减小手轮的转值。

2）系统的动态参数对调节精度有一定的影响。这种动态参数主要是指系统折算到手轮轴上的负载力矩和惯性矩。因此，在设计调节机构时应尽量减小这种影响，以避免或减少手轮操作时产生的不均匀性所引起的调节误差。为此，手轮的转值不宜过大。