平行四边形双曲柄机构的运动轨迹分析

平行四边形双曲柄机构实质上是等长连架杆平面四杆机构。其基本形式有四种，如图3-7所示。

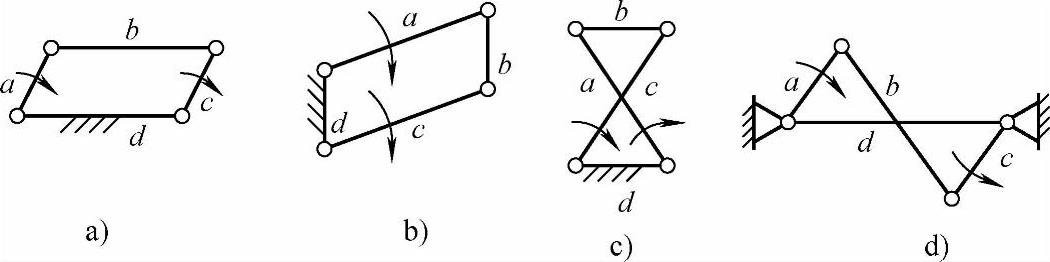
图3-7 平行四边形双曲柄机构类型

a）短曲柄同向运动平行四边形机构 b）长曲柄同向运动平行四边形机构 c）同向运动反平行四边形机构 d）反向运动反平行四边形机构

上述四种机构都存在一个共同点，即主动曲柄a转至与机架d重合时，从动曲柄c也与机架d重合。这时，机构处于死点位置，其运动方向将成为不确定状态，即此时的主动曲柄继续向前转动时，从动曲柄有可能与主动曲柄同向转动，也可能反之。

若要求从动曲柄按预定方向越过死点继续向前转动，需采取如下至少一种措施：

1）附加辅助曲柄。

2）提高杆件的质量惯性。

3）设置死点引出器。

当要求从动曲柄到达死点位置时无需越过死点而作返回转动，只需在该点设一挡块即可。

（1）同向运动平行四边形机构运动轨迹

图3-8所示的两种同向运动平行四边形机构，当曲柄a（或c）作主动转动时，从动曲柄c（或a）作同向同速转动，而连杆b均作周转变速的平移运动。

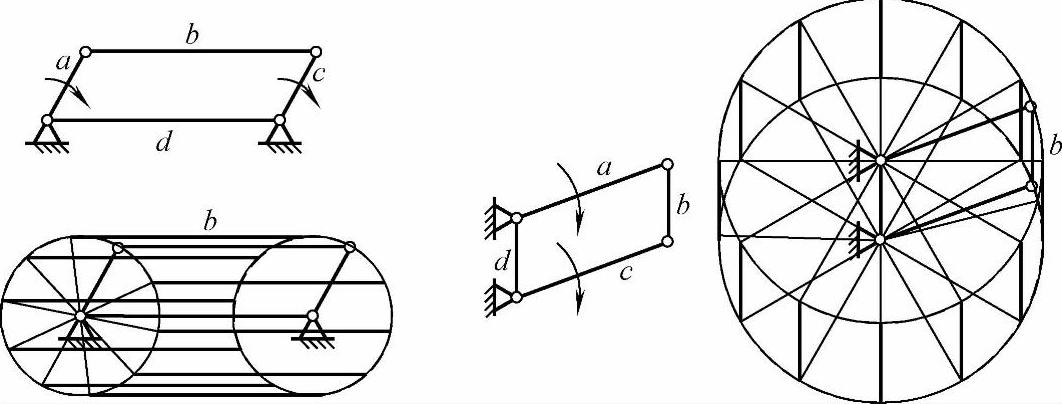
图3-8 同向运动平行四边形机构运动轨迹

图3-9所示为上述机构的连杆b的中点M及其中垂线L的运动轨迹。两者的M点的运动轨迹均是以机架d的中点为中心、以曲柄a为半径的圆。中垂线L绕机架中点作周转的平移运动。

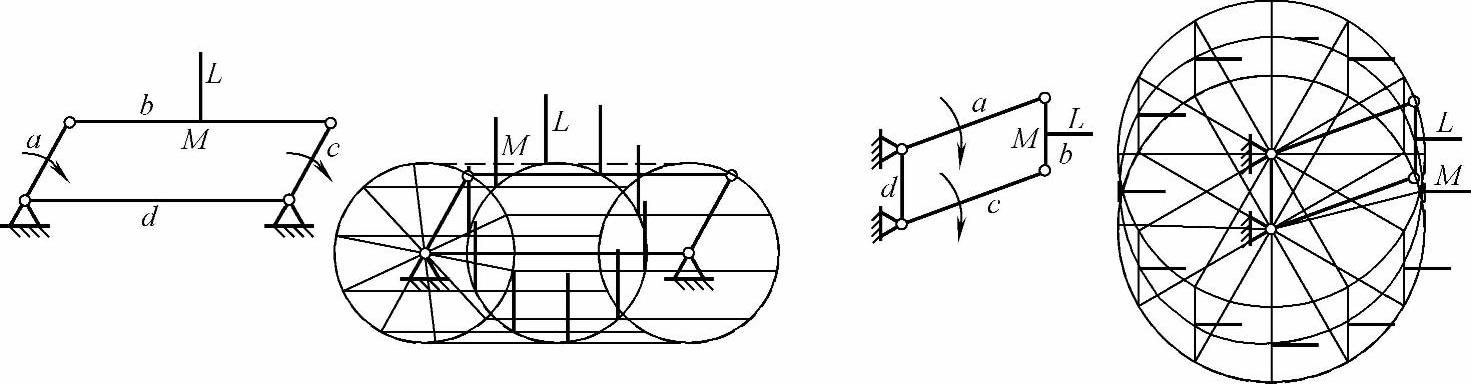
图3-9 平行四边形机构连杆中垂线运动轨迹

（2）同向运动反平行四边形双曲柄机构运动轨迹

如图3-10所示为同向运动反平行四边形双曲柄机构及其运动轨迹，该机构也是等长连架杆双曲柄机构的变形。

图3-10a所示机构的连杆b作整周的、变速的翻转运动，连杆b的中点M及杆a和杆c的交点D的运动轨迹均为椭圆，所以称为椭圆机构。

图3-10b所示机构的连杆b的中垂线端点E的运动轨迹，是一条对称于机架d的中垂线的玫瑰线形曲线。玫瑰线形曲线的极坐标方程式为：ρ=ksin（φ／3）。

图3-10c所示机构的连杆b的延长线端点E的运动轨迹，是一条对称于机架d的玫瑰线形曲线。这种玫瑰线形曲线的极坐标方程式为：ρ=kcos（φ／3）。

可见，图3-10b、c可作为玫瑰形曲线的极坐标几何计算机构。同时表明，E点运动速度的变化规律是内环慢，外环快，速度变化剧烈。

这种机构应用在速度快慢变化特殊的环形传动装置、机械手、娱乐器械及动态灯饰等。

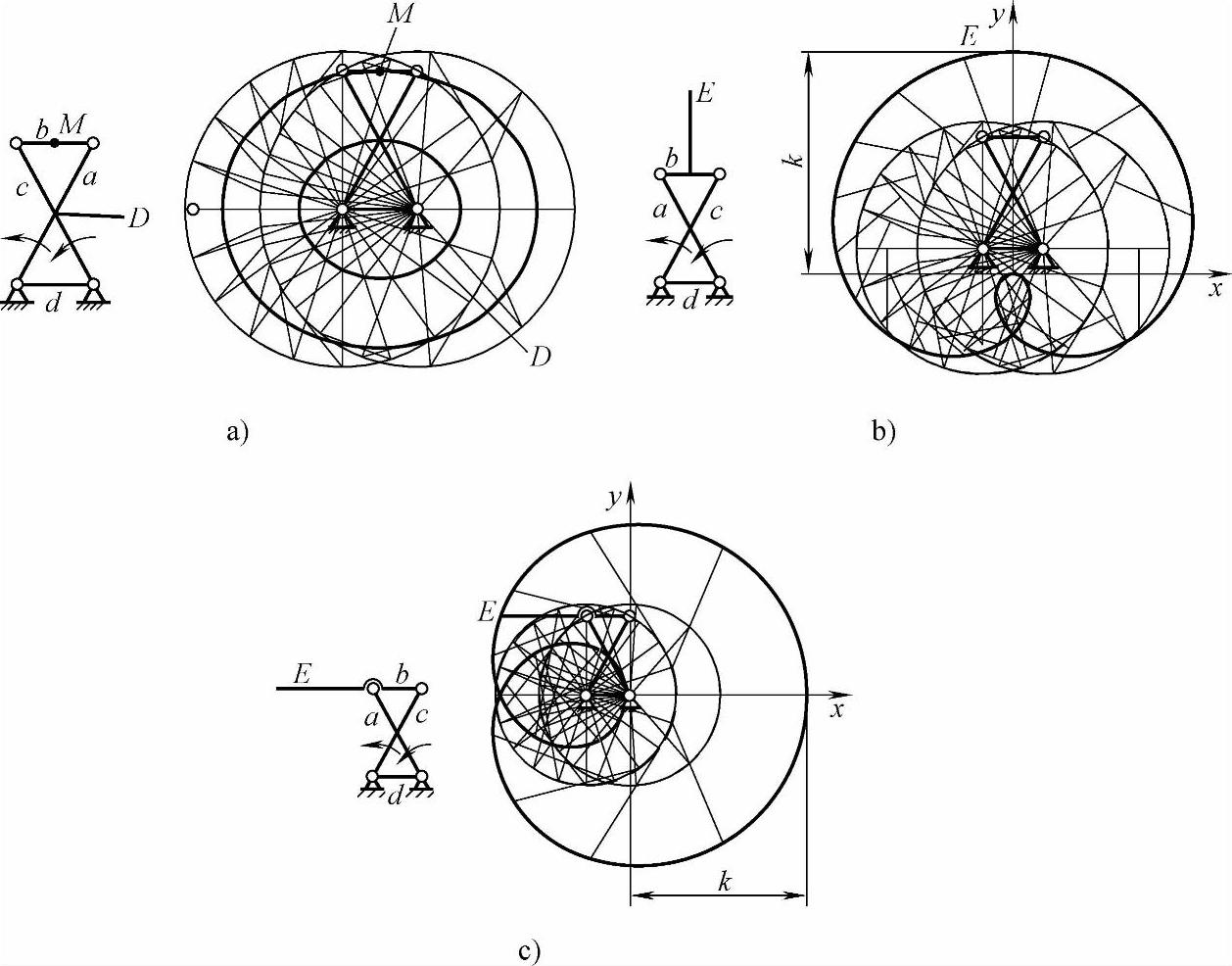
图3-10 同向运动反平行四边形机构及其运动轨迹

（3）反向运动反平行四边形双曲柄机构运动轨迹

反向运动反平行四边形机构连杆b与机架d相交叉。当主动曲柄a转到与机架d重合时，从动曲柄c因处于不确定状态，有可能继续向前转动，也可能反向转动，所以机构的运动轨迹也会出现两种状态。

1）当从动曲柄到达与机架共线的位置时，若需越过死点继续向前转动，则连杆b及其上的一些点的运动轨迹如图3-11所示。图3-11a所示的机构中，连杆b对称于机架d作往复变速移动兼摆动。图3-11b所示的机构中，连杆b的中点M及其中垂线的端点E的运动轨迹是条横8字形曲线。

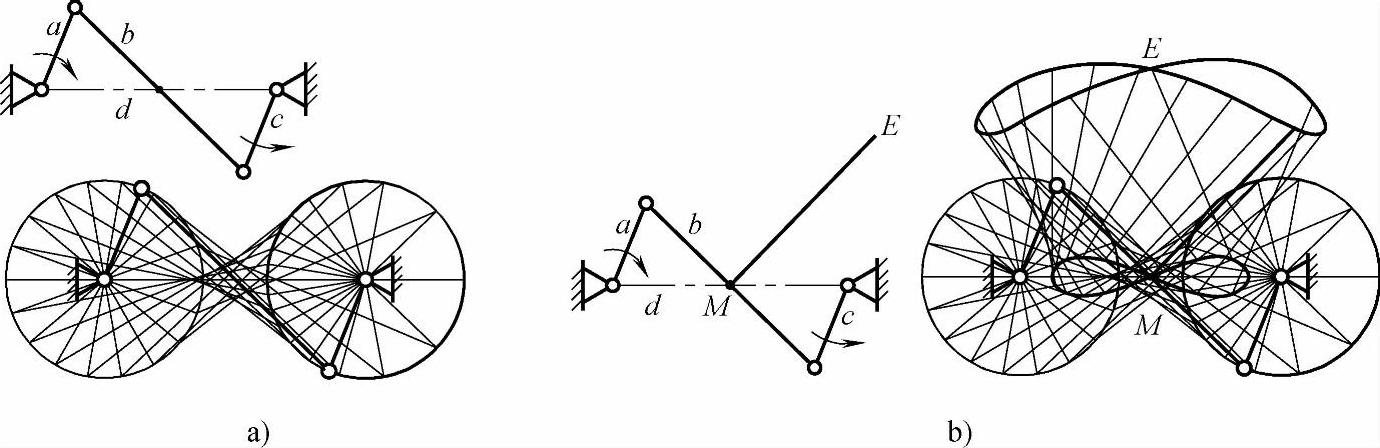
图3-11 反向运动反平行四边形机构及其运动轨迹

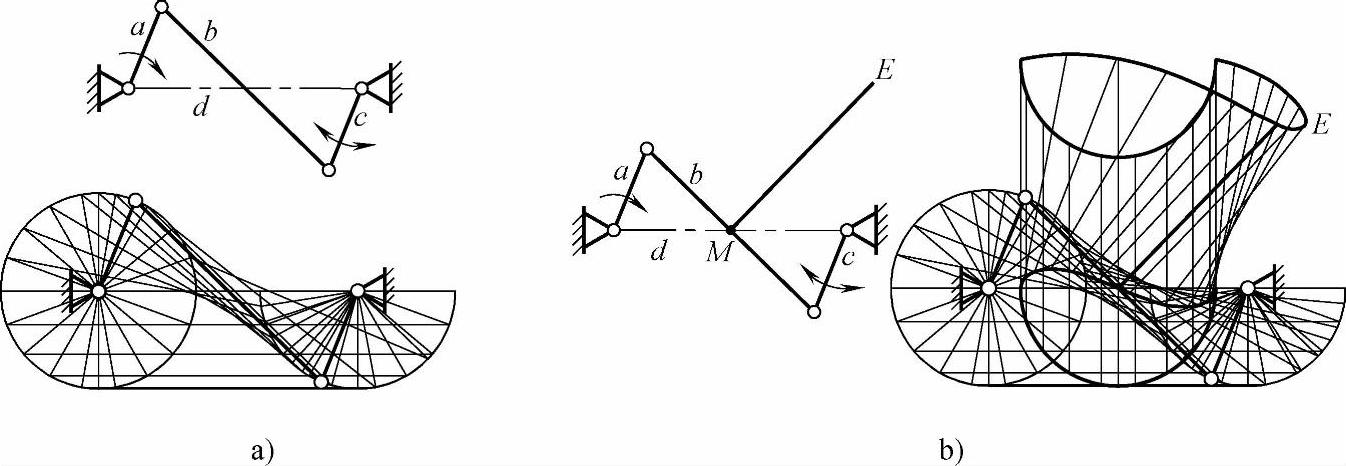
2）当从动曲柄到达与机架共线的位置时，若不越过死点而反向转动，则连杆b及其上的一些点的运动轨迹如图3-12所示。图3-12a所示的机构中，当曲柄a在机架d上半周转动时，连杆b向右作变速移动兼摆动；当曲柄a在机架d下半周转动时，连杆b在机架下方向左作变速平移运动。图3-12b所示的机构中，连杆b的中点M的运动轨迹，是由对称于机架d的半个横8字形曲线和机架下方的半个圆弧组成的曲线；连杆b的中垂线的端点E的运动轨迹是一条由半圆弧和多变曲线组成的横8字形曲线。

(www.xing528.com)

图3-12 反向运动反平行四边形机构从动曲柄不越过死点时的运动轨迹

（4）平行四边形双曲柄机构的应用

平行四边形双曲柄机构应用广泛，如物料传递机构、平移运动装置、振动机、机车传动、平衡吊装机、比例仿形机、缩放机及绘图机等。

1）物件步进传递机构。图3-13所示的物件步进传递机构由平行四边形双曲柄机构组成。曲柄3连续转动，连杆1与取料器2连在一起作平移周转运动，从而把物料4逐件步进传递至出料口。传递行程及步数可根据需要设定。

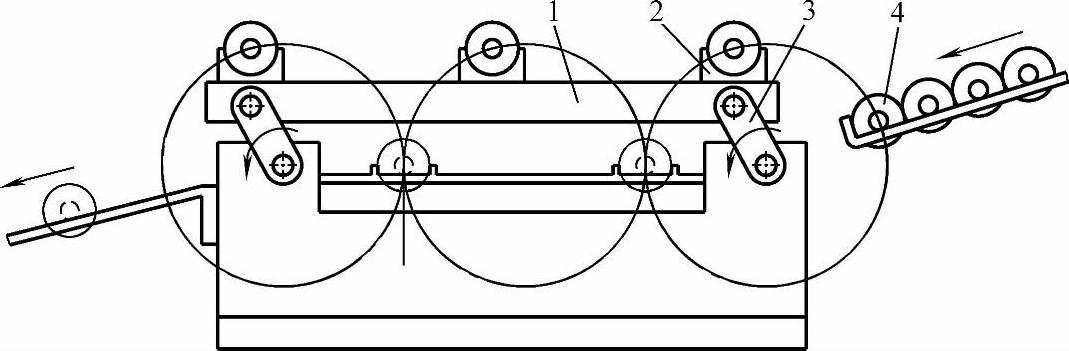
图3-13 平行四边形机构应用-步进传递物件

1—连杆 2—取料器 3—曲柄 4—物料

2）工作台周转平移运动机构。图3-14所示的物料步进传递机构由两个平行四边形双曲柄机构组成。用电动机驱动主动曲柄圆盘1转动，带动起共用连杆作用的工作台3作周转平移运动。两作用连杆的有效长度l相等。两从动曲柄2的有效长度等于曲柄圆盘的半径r。

振动台也按此原理设计，其振幅大小取决于曲柄长度r。

3）双轴同步传动机构。图3-15所示机构是由两个平行四边形双曲柄机构组成的双轴同步传动装置。用电动机驱动曲柄圆盘1带动共用连杆3，并驱动两个从动曲柄圆盘2，从而使轴A和轴B作同向等速转动。

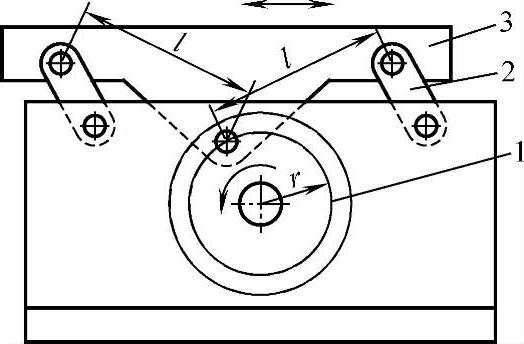
图3-14 平行四边形机构应用-工作台周转平移运动

1—曲柄圆盘 2—从动曲柄 3—工作台

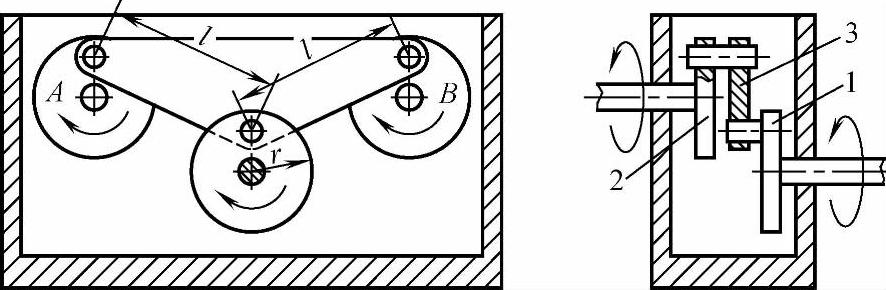
图3-15 平行四边形机构应用-双轴同步传动

1—曲柄圆盘 2—从动曲柄圆盘 3—共用连杆

同理，两作用连杆的有效长度l相等。两从动曲柄圆盘2的转动半径等于主动曲柄圆盘的转动半径r。

4）多轴同步传动机构。图3-16所示是利用四个平行四边形双曲柄机构组成的四轴同步传动装置。这种机构可用于多头钻或多头铣的设备，也可用于各种多轴同步等速的传动。

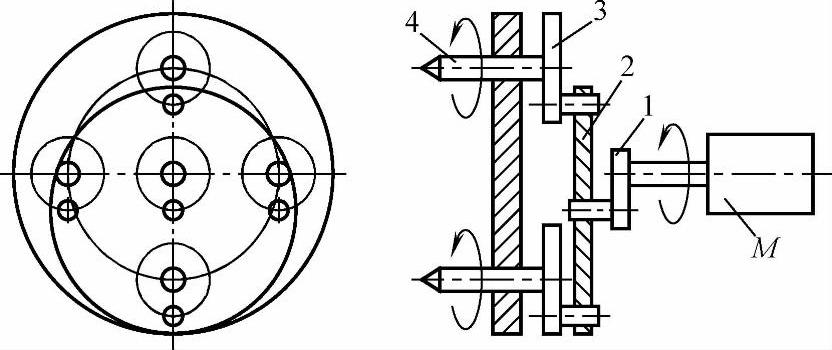
图3-16 平行四边形机构应用-多轴同步传动

1—主动曲柄 2—转盘 3—曲柄 4—输出轴

传动原理：电动机M驱动主动曲柄1连续转动，并带动发挥公共连杆作用的转盘2作周转平移运动。然后使四只等长曲柄3绕各自输出轴4作同步等速转动。各输出轴端可装上刀具（如钻头、铣刀）或其他所需的传动构件。

5）物料翻转传递机构。利用同向反平行四边形机构的翻转运动特性，可作出如图3-17所示的物料翻转传递机构。机构的主动连架杆a由摆动气缸1驱动，连杆b与料斗2铰连。料斗从A端取料，送至B端。料斗作了一个翻转运动，即把物料卸进出料槽。

6）圆弧打磨机构。图3-18所示是由三个平行四边形曲柄机构组成的复合机构，可用于圆弧打磨的设备。图3-18a所示是基本结构，d是共用机架。上、下连杆b的等长延长线与连杆l铰接，l=e，a=c。当主动曲柄a转动时，连杆l的中点M及其中垂线h的端点E的运动轨迹均为圆曲线。图3-18b所示为以图析法绘制的运动轨迹图线，可见，M点的轨迹是以l为边长的等边三角形的内切圆。

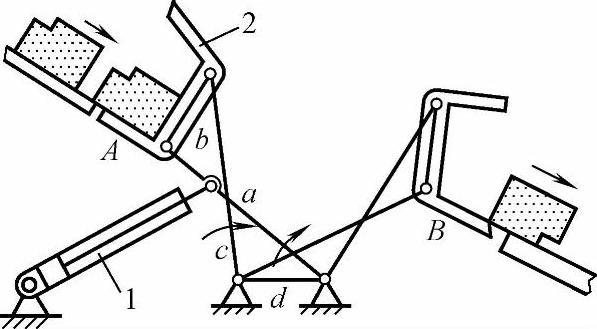
图3-17 平行四边形机构应用-物料翻转传递机构

1—摆动气缸 2—料斗

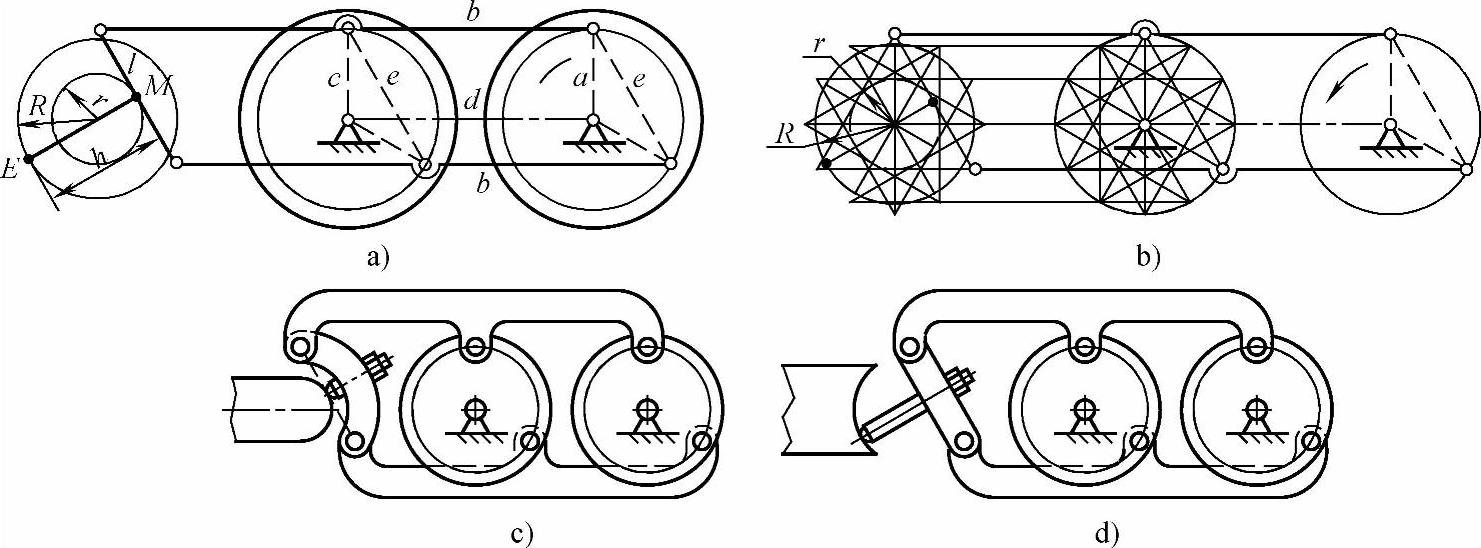
图3-18 平行四边形机构应用-圆弧打磨机构

两轨迹圆的半径r和R的关系为

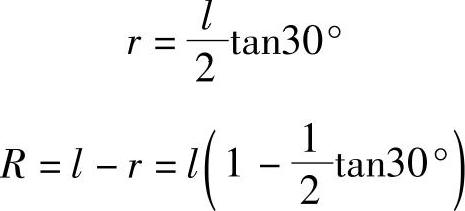
这种机构可用于如图3-18c、d所示的外圆和内圆边缘打磨的设备。当h≤r时，端点E的轨迹圆小于或等于M点的轨迹圆，适用于凸圆弧打磨；当h＞r时，端点E的轨迹圆大于M点的轨迹圆，适用于凹圆弧打磨。