如何利用卷积码提高纠错能力？

前面讨论的分组码的约束关系完全限定在各码组之内。如果需要提高分组码的纠错能力，只能增加校验码元个数，这不但降低了编码效率，同时还增加了编译码设备的复杂程度。编译码时必须把整个信息码组存储起来，由此产生的延时随着n的增加而线性增加。遇到既要求n、k较小，又要求纠错能力较强的情况，可选择卷积码。

由于卷积码充分利用了各码组之间的相关性，n和k可以选得很小，因此在与分组码同样的传信率和设备复杂性相同的条件下，卷积码的性能比分组码好。缺点是，对卷积码的分析至今还缺乏像分组码那样有效的数学工具，往往要借助于计算机才能搜索到一些好码的参数。

1.卷积码的编码

在卷积码中，一个码组（子码）的监督码元不仅与当前子码的信息码元有关，而且与前面N-1组子码的信息码元有关，所以各码组的监督码元不仅对本码组而且对前N-1组内的信息码元也起监督作用，因此要用（n，k，N）三个参数表示卷积码。其中n表示子码长度；k表示子码中信息码元的个数；N为编码约束长度，用以表示编码过程中相互约束的子码个数；N·n为编码过程中相互约束的码元个数。卷积码的纠错能力随着N的增加而增大，差错率随着N的增加而呈指数下降。

（n，k，N）卷积码的编码效率R=k/n。如果卷积码的各子码是系统码，则称该卷积码为系统卷积码。假如N=1，那么卷积码就是（n，k）分组码了。

卷积码编码器由N个k级的移位寄存器和n个模2加法器组成。一般形式如图1-5-5所示。

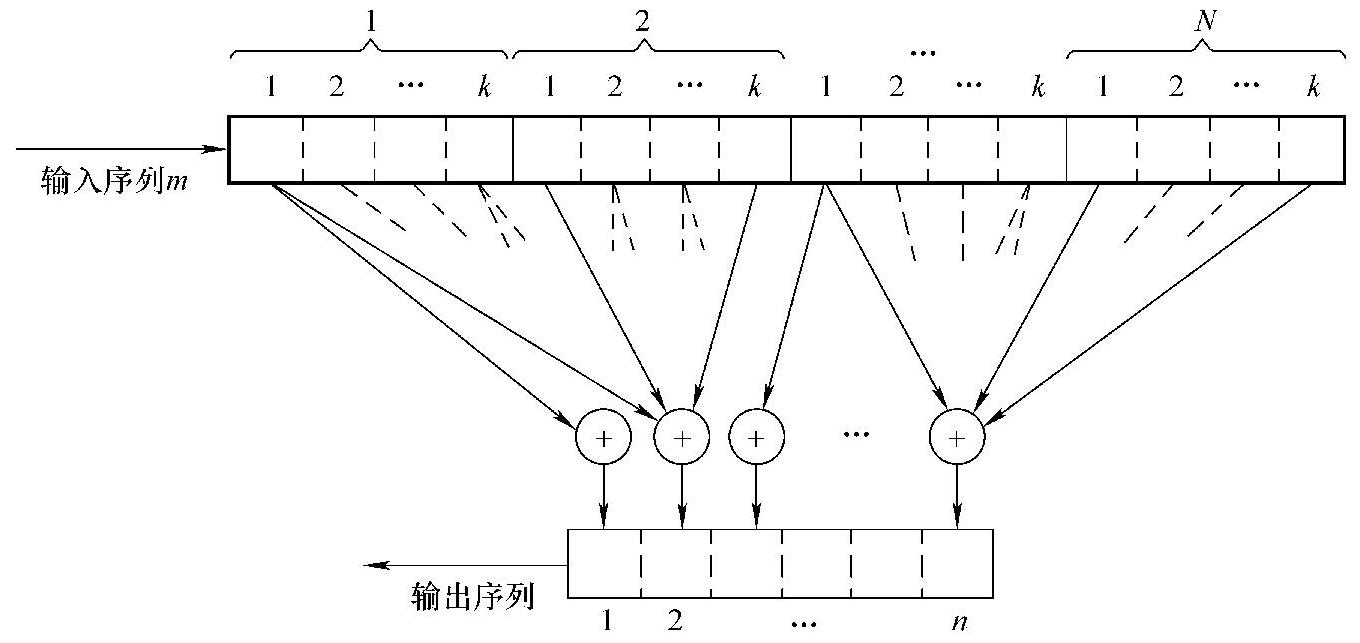
图1-5-5 卷积码编码器的一般形式

图1-5-6所示为一个（2，1，3）卷积码编码器。此编码器与输入、输出的关系以及各子码之间的约束关系如图1-5-7所示。

2.卷积码的描述

描述卷积码的方法有两类：解析表示和图解表示。

（1）卷积码的解析表示

一般有两种解析表示法描述卷积码，它们是移位算子（延迟算子）多项式表示法和半无限矩阵表示法。在移位算子多项式表示中，编码器中移位寄存器与模2加的连接关系以及输入、输出序列都表示为移位算子x的多项式。

（2）卷积码的图解表示

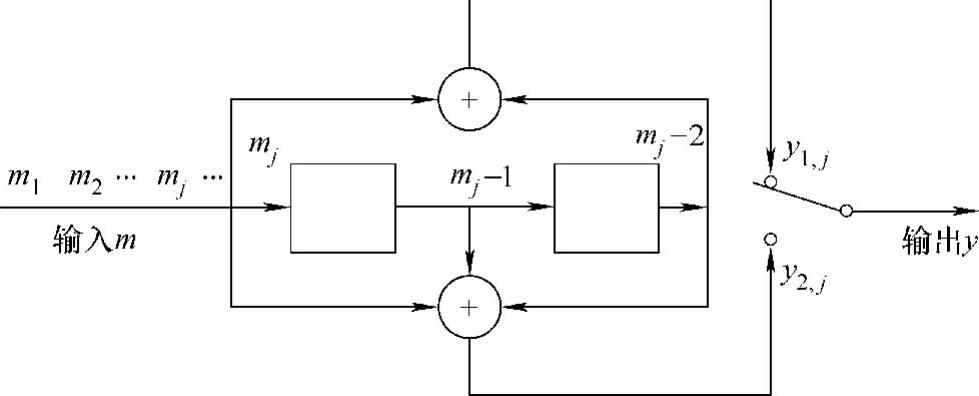
图1-5-6 （2，1，3）卷积码编码器

卷积码编码过程有三种图解表示方法，即树状图、网格图和状态图。

1）树状图

图1-5-7 输入、输出关系和各子码之间的约束关系

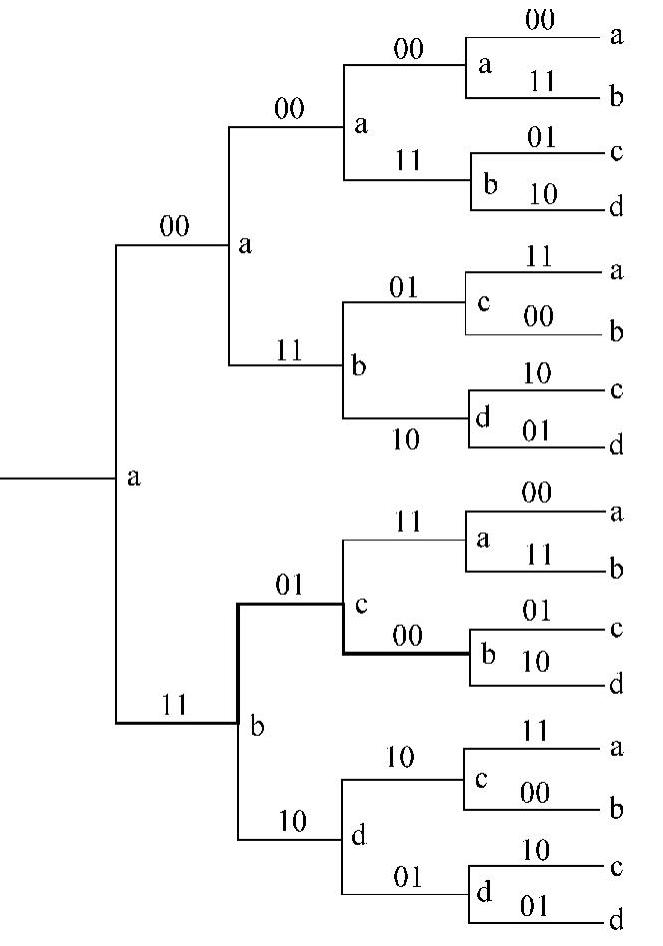
图1-5-8 （2，1，3）卷积码的树状图(www.xing528.com)

如前所述，对不同的输入信息可以利用上述解析方法求出输出码序列。若将这些序列画成树枝形状就得到树状图或叫作码树图，并且码树可一直向右延伸，所以又称半无限码树图。它描述了输入任何信息序列时，所有可能的输出码字。与图1-5-7（2，1，3）编码电路对应的码树画于图1-5-8中。图中每个分支表示一个输入符号。通常输入码元为0对应上分支，输入码元为1对应下分支。每个分支上面标示着对应的输出，从第三级支路开始码树呈现出重复性（自上而下重复出现a、b、c、d四个节点），表示从第4位数据开始，输出码字已与第1位数据无关，它解释了编码约束度（m=N+1）的含义。

2）网格图

如果把码树中具有相同状态的节点合并，就可以得到网格图。与码树中的规定相同，输入码元为0对应上分支（用实线表示）；输入码元为1对应下分支（用虚线表示）。网格图中支路上标注的是输出码元（见图1-5-9）。

3）状态图

状态图表示的是编码器中移位寄存器存数状态转移的关系。上述（2，1，3）卷积码k=1，寄存器级数为2，所以有4级状态00、01、10、11分别记为a、b、c、d，与其对应的状态图如图1-5-10所示。状态转移路线上端的数字表示输入信息码元，状态转移路线下端的数字表示与其对应的输出。

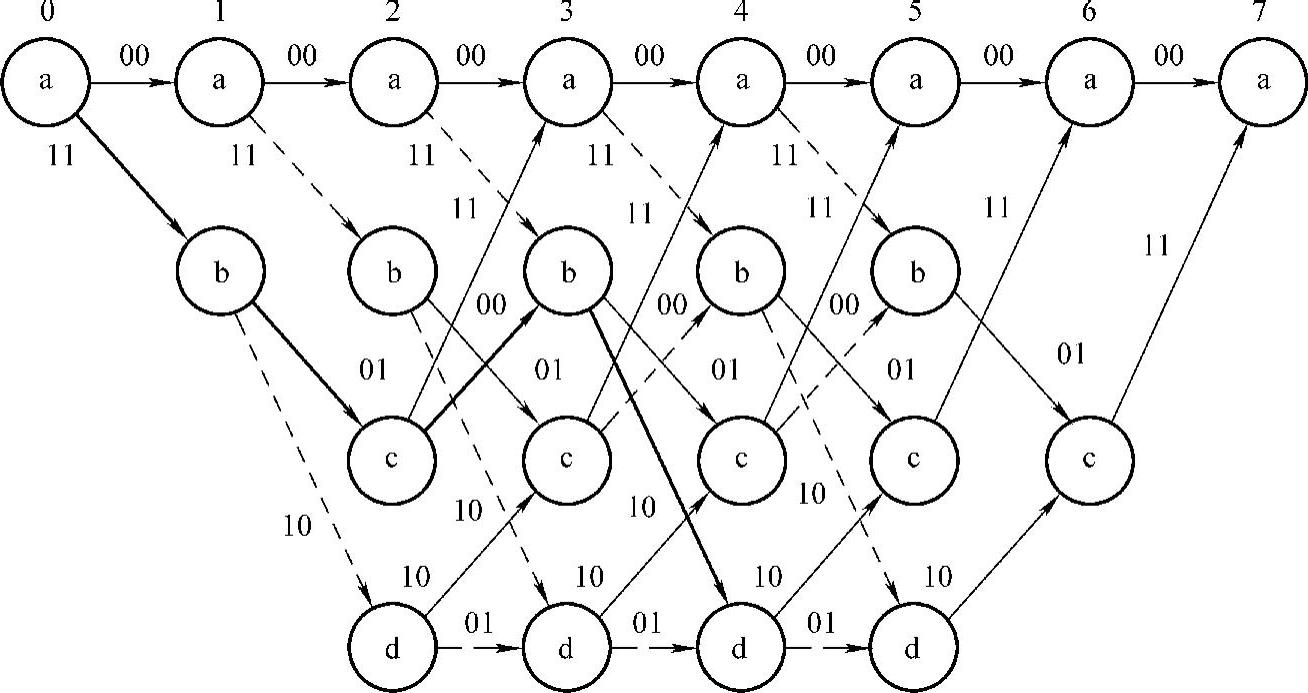
图1-5-9 （2，1，3）卷积码的网格图

以输入1011为例，移位寄存器的状态由初始状态a依次变化为b、c、b、d，相应的输出码元序列仍然是11010010。上述三种图解表示方法，都是以图1-5-6所示的（2，1，3）编码电路的卷积码为例给出的。

对于一般的（n，k，N）卷积码，可以由此推广出来以下结论：

（1）对应于每组k个输入比特，编码后产生n个输出比特。

（2）树状图中每个节点引出2k条支路。

（3）网格图和状态图都有2k（N-1）种可能的状态。每个状态引出2k条支路，同时也有2k条支路从其他状态或本状态引入。

3.卷积码的译码

（1）卷积码的距离特性

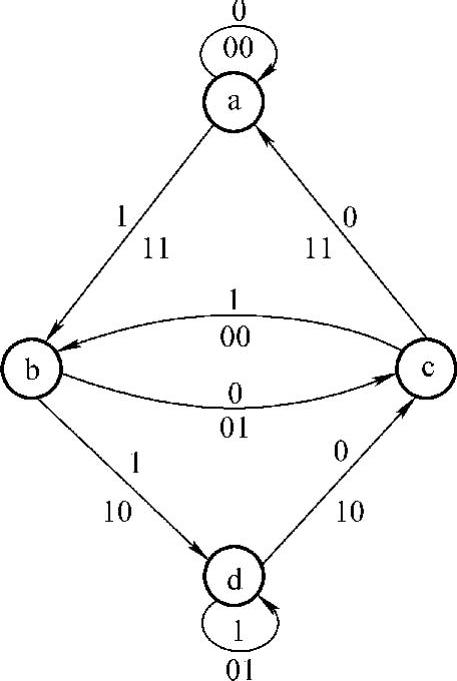
图1-5-10 （2，1，3）卷 积码的状态图

同分组码一样，卷积码的纠错能力也由距离特性决定，但卷积码的纠错能力与它采用的译码方式有关，因此不同的译码方法就有不同的距离度量。称长度为N·n的编码序列之间的最小汉明距离为最小距离d_min；称任意长的编码序列之间的最小汉明距离为自由距离d_free。由于卷积码并不划分为码字，因而以自由距离作为纠错能力的度量更为合理。对于卷积码中广泛采用的维特比译码算法，自由距离d_free是个重要参量。一般情况下，在卷积码中d_min≤d_free。

（2）卷积码的译码

卷积码的译码分为代数译码和概率译码两大类。卷积码发展的早期多采用代数译码，现在概率译码已越来越被重视。概率译码算法主要有维特比译码和序列译码。由于维特比译码在通信中用得更为广泛，这里仅简单介绍维特比译码。

维特比译码算法采用的是最大似然算法。它把接收码序列同所有可能的码序列作比较，选择一种码距最小的码序列作为发送数据。