如何使用奇偶校验码进行数据校验？

分组码是信道编码后的序列可分为n个码元一组，其中k个码元是信息码，r=n-k个码元是附加的监督码元。在分组编码中，监督码元仅与本组的信息码元有约束关系。

分组码常用（n，k）来表示，它是将k位信息码元，经编码后形成n位一组的输出序列（n>k），其中附加的r=n-k位是监督码元，其编码效率R=k/n。分组码中的监督码元只与本组中的信息码元有监督约束关系。输入的k位信息组合共有2^k个不同的形式，编码器输出也只需对应这2^k个输入形式输出2^k个不同的码组即可。但由n位二进制数组成的序列组合，共有2ⁿ个不同的形式，因此，（n，k）分组编码就是从这2ⁿ个二进制数组合中，挑选出2^k个作为编码的输出码组（也称为许用码组或码字），其余的（2ⁿ-2^k）个则是禁用码组。当信道编码输出的码字在信道中传输时，产生的误码就可能使原来的许用码组变为禁用码组，这时接收端就可判断出此码组中有误码，但误码也可能使一个许用码组变为另一个许用码组，这时，接收端就无法判断出有误码。分组码的检、纠错能力与码组中附加的监督码元个数有关，当r越大，禁用码组越多，误码使许用码组变为禁用码组的可能性越大，则编码的检、纠错能力越强，但同时，附加的与传输信息无关的码元个数增加了，因此，在实际应用中要折中考虑数据率和差错控制编码的检纠错能力。

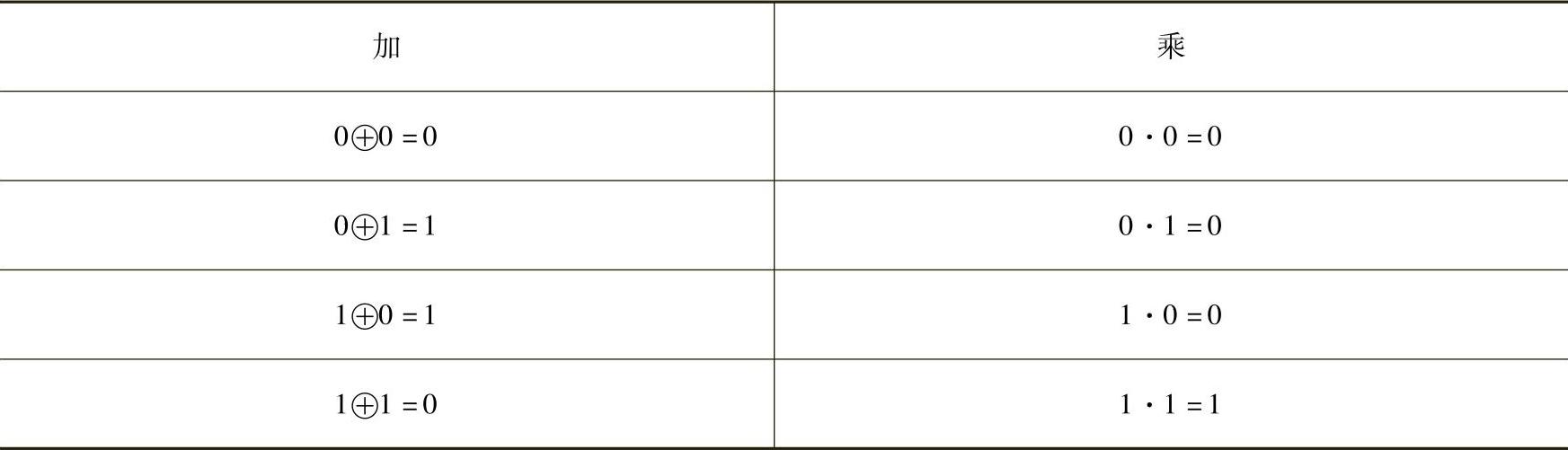
从代数学的角度，每个二进制码组可以看成是只有0和1两个元素的二元域中的n重。所有二元n重的集合称为二元域上的一个矢量空间。二元域上只有两种运算，即加和乘，所有运算结果也必定在同一个二元集合中。在二元域中加和乘的运算规则见表1-5-2。

表1-5-2 二元域运算规则

奇偶校验码是分组码。它是在一组信息码元之后附加一位监督码元，组成一组满足奇校验关系或偶校验关系的码组。当附加的监督码元使码组中“1”的个数为偶数时，称为偶校验码，即偶校验码码组中的码元满足下面的约束关系

S=a_n-1⊕a_n-2⊕…⊕a₀

式中，a₀是监督位；其他n-1个码元为信息码元。(www.xing528.com)

a_n-1⊕a_n-2⊕…⊕a0=0 （1-5-4）当附加的监督码元使码组中“1”的个数为奇数时，称为奇校验码，则奇校验码码组中的码元满足关系为

a_n-1⊕a_n-2⊕…⊕a0=1 （1-5-5）

式（1-5-4）和式（1-5-5）也称为监督关系式。

奇偶校验码的编码率为R=（n-1）/n。

表1-5-3显示了对两位信息码元进行奇偶校验编码的结果。码组中的前两位是信息位，与原信息码完全相同，第三位是监督位。奇校验码和偶校验码均可检测奇数个误码。在接收端，译码器将码组中各码元相加（模2和），若结果满足监督关系式，则判断无误码，反之，则认为有误码。例如，若接收端收到一个奇校验码的码组序列为1100101，由于，1+1+1+0+1+0+1=0，不满足奇校验码的约束关系式（1-5-5），由此可判断此码组中有误码，但无法判断出是哪一位发生了错误，因此，奇校验码是检错码，无纠错的能力。偶校验码与奇校验码有同样的检纠错的能力。

表1-5-3 奇偶校验码