Matlab的符号运算工具箱提供了许多符号运算的功能，例如求解函数的微分、积分，求解代数方程的解析解等等。本节主要介绍利用符号运算功能进行拉氏变换和逆变换。
在利用符号运算工具箱求解问题时，必须首先用syms命令来声明符号变量。如果没有声明，Matlab将把该变量当成一般数值变量，从而得不到正确结果。下面的例子给出了声明符号变量的形式
此时变量a，b，t，d，e，y被定义为符号变量。注意在syms命令中，各个变量之间是不加逗号的。
符号运算工具箱中提供了两个函数，laplace（）和ilaplce（），利用这两个函数可以分别求解Laplace变换及其逆变换。
例M-4 求解函数e﹣btcos（at＋c）的拉氏变换。
解 相应的Matlab运行结果如下
即输出为
例M-5 求函数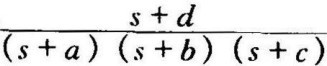
的拉氏反变换。
解 Matlab解为
转换成一般形式为
例M-6求函数
的拉氏反变换。
解 Matlab解为
转换成一般形式为
4e﹣4t－6e﹣3t＋2e 2t＋e﹣t
Matlab符号运算工具箱ver2.1.2功能有了较大改进，原先有的不能直接计算的结果，现在也可以得出结果了。下面两个例子在以前的低版本符号运算工具箱中，不能得到解析解，但使用Matlab6.0时，可以得到解析解。
例M-7 求解函数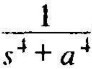
的拉氏反变换。
解
转换成一般形式为
例M-8 求解函数
的拉氏反变换。
解
转换成一般形式为
例M-9 求解函数
的拉氏反变换。
解 Matlab解为
由此看出，得不到解析解，因为5次以上的代数方程一般没有解析解。此时，可利用求根函数，求出系统的极点。
＞＞roots（[1，2，3，4，5，6]）
ans＝(www.xing528.com)
0.5517＋1.2533j
0.5517－1.2533j
﹣1.4918
﹣0.8058＋1.2229j
﹣0.8058－1.2229j
其近似拉氏反变换可以写成
使用pfrac函数，可以得出系统的部分分式表达式，从而得到更为简洁的结果。
[P，R，K]＝pfrac（1，[1，2，3，4，5，6]）
P＝
0.0885＋0.0000j
﹣0.1521
3.1289
﹣0.0868
1.4997
R＝
﹣1.4918
﹣0.8058＋1.2229j
﹣0.8058－1.2229j
0.5517＋1.2533j
0.5517－1.2533j
K ＝
[]
其结果的数学表达式为
0.0885e﹣1.4918t－0.1521e﹣0.8058tsin（1.2229t＋3.1289）﹣0.0868e1.4997tsin（1.2533t＋1.4997）
函数pfrac源程序如下
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
