考虑具有如下不确定性的被控对象
其中xp(t)是n维的状态向量,u(t)是m维的控制向量,y(t)是l维的输出向量;Ap, Bp,Cp,Dp是已知的具有适当维数的常数矩阵,且(Ap,Bp)完全可控制,(Cp,Ap)完全可观测;A△,B△,C△,D△是具有适当维数的常数或者时变矩阵,表示系统的不确定性并且满足关系
∣∣A△xp(t)∣∣≤βA∣∣xp(t)∣∣,∣∣B△u(t)∣∣≤βB∣∣u(t)∣∣
∣∣C△xp(t)∣∣≤βC∣∣xp(t)∣∣,∣∣D△u(t)∣∣≤βD∣∣u(t)∣∣ (10-15)
其中xp(t)表示状态向量xp(t)各分量的绝对值之和, 其他∣∣u(t)∣∣,∣∣A△xp(t)∣∣,∣∣B△u(t)∣∣,∣∣C△xp(t)∣∣,∣∣D△u(t)∣∣的意义与之相同。
其他∣∣u(t)∣∣,∣∣A△xp(t)∣∣,∣∣B△u(t)∣∣,∣∣C△xp(t)∣∣,∣∣D△u(t)∣∣的意义与之相同。
反馈控制器取为
其中xc(t)是q维的控制器状态向量,Ac,Bc,Kp,Kc是已知的具有适当维数的常数矩阵。当Kp=0时,上式是单一的动态输出反馈控制器;而当Kc=0时,上式退化为普通的状态反馈控制器u(t)=Kpxp(t)。若控制器式(10-16)不仅能使标称的闭环系统稳定,并且能保持实际的不确定性系统(10-14)也稳定,则闭环系统具有稳定鲁棒性。
将式(10-16)代入式(10-14),得到闭环系统的状态方程为
其中
被控对象无参数不确定性时(A△=B△=C△=D△=0),闭环系统的状态转移矩阵为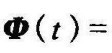
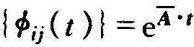 ,若系统稳定则存在常数m,a>0使下式成立
,若系统稳定则存在常数m,a>0使下式成立
将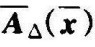 视为闭环系统(10-17)的输入,则闭环系统的状态响应
视为闭环系统(10-17)的输入,则闭环系统的状态响应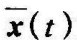 为
为
于是有
由式(10-15)、式(10-16)和式(10-17)可有
记ρA=βA+(βB+βD∣∣Bc∣∣)·∣∣[KpKc]∣∣+βC∣∣BC∣∣,则有 其中∣∣Bc∣∣和∣∣[KpKc]∣∣的定义与式(10-18)类似。同样的还可有
其中∣∣Bc∣∣和∣∣[KpKc]∣∣的定义与式(10-18)类似。同样的还可有
其中ρC=βC+βD∣∣[KpKc]∣∣。
将式(10-18)和式(10-21)代入式(10-20)得到
于是有
根据Bellman-Gronwall引理[1],有
于是
由式(10-17)、式(10-22)和式(10-24)有(https://www.xing528.com)
由式(10-17)、式(10-24)和式(10-25)可知,若设计控制器(10-16)能够使得闭环系统矩阵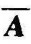 的特征值都具有负实部,即
的特征值都具有负实部,即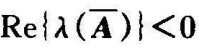 ,并且成立关系
,并且成立关系 ,则闭环系统对于模型摄动A△,B△,C△,D△具有稳定鲁棒性。
,则闭环系统对于模型摄动A△,B△,C△,D△具有稳定鲁棒性。
例10-5 已知动态系统的线性数学模型为
控制器为
若系统矩阵存在偏差
试分析闭环系统的稳定鲁棒性。
解 由给定的参数有
∣∣A△xp(t)∣∣≤0.46∣∣xp(t)∣∣
于是有
βA=0.46,βB=0,βC=0,βD=0
ρA=βA+(βB+D∣∣Bc∣∣)∣∣[KpKc]∣∣+βC∣∣BC∣∣=βA=0.46
闭环系统为
闭环系统的特征值为﹣3,﹣4,﹣6,﹣8。状态转移矩阵为
图10-9中sum1,sum2,sum3,sum4分别是状态转移矩阵Φ(t)各列元素绝对值之和随时间变化的曲线,与3.61e﹣1.7t的曲线相比之后可知有如下关系成立。
图10-9 状态转移矩阵各列元素绝对值之和随时间变化的曲线
于是有a=1.7,m=3.61,成立关系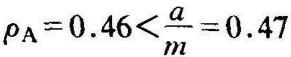 ,闭环系统对于模型摄动A△具有稳定鲁棒性。
,闭环系统对于模型摄动A△具有稳定鲁棒性。
由式(10-26)可知实际的闭环系统矩阵为
它的特征值为﹣2.0328,﹣7.6051,﹣6.1800,﹣4.6020,实际闭环系统稳定。
[1]Bellman-Gronwall引理:设f(t),x(t)是[t0,∞)上的连续函数,而M,N是非负常数,若 则有
则有 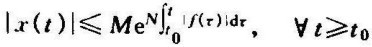
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




