传递函数不确定性对稳定鲁棒性的影响

控制系统模型的不确定性不仅仅局限于参数不确定性。在图10-4所示的反馈系统中，被控对象为

P（s）＝P0（s）（1＋P△） （10-10）

图10-4 不确定性反馈控制系统

其中P0（s）是标称模型，P△表示模型中的不确定部分，它未知但稳定并且满足关系

W（s）是一个稳定的已知传递函数。由式（10-10）和（10-11）可有

∣W（jω）∣代表了模型相对不确定性的上界。

设控制器C（s）使标称系统闭环稳定，则P0（s）C（s）（1＋P0（s）C（s））﹣1是稳定的传递函数，又已经假设P△（s）稳定，所以由奈奎斯特稳定判据可知闭环系统稳定的充分条件是

记T（s）＝P0（s）C（s）（1＋P0（s）C（s））﹣1，则闭环系统稳定鲁棒的充分条件为

例10-3 设标称被控对象为

当控制器取为常数增益C1（s）＝115时，系统的闭环极点是｛﹣0.08，﹣12.67，﹣0.13± 100.13j｝，系统稳定。设实际的被控对象中含有未建模因子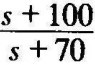，在式（10-10）中则有

作T（s）和1/W（s）的对数幅频特性，由图10-5可见系统不满足鲁棒稳定条件（10-13），因此实际系统可能是不稳定的。经验算，实际闭环系统的极点是

｛﹣0.0827，﹣18.1199，﹣66.1944，0.6985±99.2522j｝

有两个右半S平面的极点，系统的确不稳定。(www.xing528.com)

将控制器改用滞后校正网络

图10-5 例10-3中采用C1（s）时T（jω）和1/W（jω）的对数幅频特性

这时T（s）和1/W（s）的对数幅频特性如图10-6所示，显然能够满足式（10-13）。验算后可知这时实际闭环系统的极点是｛﹣0.0832，﹣69.7927，﹣4.4693±99.6388j，﹣3.3428± 5.5814j｝，系统对给定的模型不确定性具有稳定鲁棒性。

图10-6 例10-3中采用C2（s）时T（jω）和1/W（jω）的对数幅频特性

例10-4 被控对象的标称模型和采用的控制器均与例10-3中的相同，仅设实际被控对象中含有的未建模因子是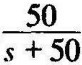，这时在式（10-10）中有

采用控制器C1（s）和C2（s）后，实际闭环系统的极点分别为

｛﹣0.0770，﹣17.9523，﹣36.9371，﹣4.0168±97.7494 j｝

和

｛﹣0.0775，﹣49.5428，﹣2.9811±4.8038j，﹣4.9588±99.6495j｝

两种情况下系统对模型摄动50/（s＋50）均具有稳定鲁棒性。两种情况下T（s）和1/W（s）的对数幅频特性分别如图10-7和图10-8所示，但由图10-7可见采用控制器C1（s）时并不满足式（10-13）的稳定鲁棒性条件，其原因在于对给定的模型摄动，式（10-13）仅是稳定鲁棒的充分条件，而非必要条件。

图10-7 例10-4中采用C1（s）时T（jω）和1/W（jω）的对数幅频特性

图10-8 例10-4中采用C2（s）时T（jω）和1/W（jω）的对数幅频特性