【摘要】：俄国学者Kharitonov在1978年发表了关于区间多项式稳定性研究的开创性工作，他指出可以通过检查4个多项式的赫尔维茨性来判别区间多项式族中无穷多个多项式是否为赫尔维茨多项式。Kharitonov多项式为利用劳斯判据检验后可知4个Kharitonov多项式都是赫尔维茨的，所以在参数范围0.5≤g≤2，0≤θ≤0.2内闭环系统是稳定的。
定义区间多项式族
f（s）＝αnsn＋αn－1sn－1＋⋯＋α1s＋α0（10-5）
其中系数属于如下区间
当多项式f（s）＝αnsn＋αn－1sn－1＋⋯＋α1s＋α0所有的根都具有负实部时，称它是赫尔维茨多项式。俄国学者Kharitonov在1978年发表了关于区间多项式稳定性研究的开创性工作，他指出可以通过检查4个多项式的赫尔维茨性来判别区间多项式族中无穷多个多项式是否为赫尔维茨多项式。这大大简化了参数不确定系统稳定性的判定工作。
定理10-1（Kharitonov定理） 区间多项式族（10-5）全体都是赫尔维茨多项式的充分必要条件是如下定义的4个Kharitonov多项式
都是Hurωitz多项式
例10-2 将Kharitonov定理应用于例10-1，例中不确定闭环系统的特征多项式是(www.xing528.com)
f（s）＝θT0s4＋（θ＋T0）s3＋s2＋gTdks＋gk
其中k＝1，
，T0＝0.1，不确定性参数g和θ有界
于是特征多项式各系数满足
设0≤θ≤0.2，0.5≤g≤2，即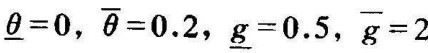
。 Kharitonov多项式为
利用劳斯判据检验后可知4个Kharitonov多项式都是赫尔维茨的，所以在参数范围0.5≤g≤2，0≤θ≤0.2内闭环系统是稳定的。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
