使用劳斯判据分析参数不确定系统的稳定区域

下面通过一个简单的例子来说明如何利用传统控制理论中的Routh判据分析具有参数不确定性的低阶系统的稳定区域。

例10-1 在图10-1所示的反馈系统中被控对象的传递函数为

其中增益g的精确值未知，供设计时使用的标称值是g＝1，θ是寄生时间常数，标称值为θ0＝0，即标称系统是

图10-1 负反馈控制系统

图10-2 校正后系统的单位阶跃响应曲线

选用控制器

当取k＝1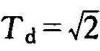，，T0＝0.1时，闭环系统有一个负实数极点﹣8.4697，和一对主导极点﹣0.7652±j0.7715，系统稳定并有如图10-2所示满意的单位阶跃响应曲线。

但是，基于标称模型（10-2）设计出来的控制器（10-3）是要用来控制实际被控对象式（10-1）的，这时闭环系统还能保持稳定吗？

实际系统的闭环特征多项式为(www.xing528.com)

系统特征值（极点）与不确定参数之间的直接关系一般很难确定，但是对于简单的情况可以使用劳斯判据确定闭环系统稳定时不确定参数的允许变化范围。列劳斯表如下

其中

察看闭环特征多项式（10-4）可知闭环系统稳定的必要条件是参数g，θ都大于零，这同时也使得劳斯表第1列中的第1，2，5个数均大于零。为使b0，b1大于零，g还需要满足g＜g1（θ）和g＜g2（θ），其中

图10-3给出了g1（θ）和g2（θ）的曲线，图中的阴影部分是闭环系统的稳定区域。但是θ＝0时需要单独考虑，这时系统的特征方程为

由劳斯判据可知对任意g＞0系统都是稳定的。

系统参数取名义值g0＝1，θ0＝0时，由图10-3可以看出系统具有较强的稳定鲁棒性。

当系统的不确定参数个数多于2个时，像这样通过解析的方法得出稳定性区域一般是不太容易的，即便是能够求出结果，也可能十分复杂而无法使用。这时需要利用下面的Kharitonov定理进行分析。

图10-3 系统的稳定区域