李雅普诺夫稳定性理论解析

（1）李雅普诺夫第一法

第一法包括了利用微分方程显式解进行系统分析的所有步骤。基本思路是：首先将非线性系统线性化，然后计算线性化方程的特征值，最后则是判定原非线性系统的稳定性。其结论如下。

①若线性化系统的系数矩阵A的特征值全部具有负实部，则实际系统就是渐近稳定的。线性化过程被忽略的高阶导数项对系统的稳定性没有影响。

②若线性化系统的系数矩阵A的只要有一个实部为正的特征值，则实际系统就是不稳定的，与线性化过程被忽略的高阶导数项无关。

③若线性化系统的系数矩阵A的特征值中，即使只有一个实部为零，其余的都具有负实部，此时实际系统不能依靠线性化的数学模型判别其稳定性。这时系统稳定与否，与被忽略的高阶导数项有关，必须分析原始的非线性数学模型才能决定其稳定性。

（2）李雅普诺夫第二法

第二法不需求出微分方程的解，也就是说，采用李雅普诺夫第二法，可以在不求出状态方程解的条件下，确定系统的稳定性。由于求解非线性系统和线性时变系统的状态方程通常十分困难，所以这种方法显示出极大的优越性。

尽管采用李雅普诺夫第二法分析非线性系统的稳定性时，需要相当的经验和技巧，然而当其他方法无效时，这种方法却能解决非线性系统的稳定性问题。

由力学经典理论可知，对于一个振动系统，当系统总能量（正定函数）连续减小（这意味着总能量对时间的导数必然是负定的），直到平衡状态时为止，则振动系统是稳定的。

李雅普诺夫第二法是建立在更为普遍的情况之上的，即：如果系统有一个渐近稳定的平衡状态，则当其运动到平衡状态的吸引域内时，系统存储的能量随着时间的增长而衰减，直到在平稳状态达到极小值为止。然而对于一些纯数学系统，毕竟还没有一个定义“能量函数”的简便方法。为了克服这个困难，李雅普诺夫引出了一个虚构的能量函数，称为李雅普诺夫函数。当然，这个函数无疑比能量更为一般，并且其应用也更广泛。实际上，任一纯量函数只要满足李雅普诺夫稳定性定理（见定理9-4和9-5）的假设条件，都可作为李雅普诺夫函数。

李雅普诺夫函数与x1，x2，⋯，xn和t有关，这里用V（x1，x2，⋯，xn，t）或者V（x，t）来表示李雅普诺夫函数。如果在李雅普诺夫函数中不含t，则用V（x1，x2，⋯，xn）或V（x）表示。在李雅普诺夫第二法中，V（x，t）和其对时间的导数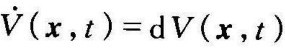/dt的符号特征，提供了判断平衡状态处的稳定性、渐近稳定性或不稳定性的准则，而不必直接求出方程的解（这种方法既适用于线性系统，也适用于非线性系统）。

①关于渐近稳定性。

可以证明，如果x为n维向量，且其纯量函数V（x）正定，则满足

V（x）＝C

的状态x处于n维状态空间的封闭超曲面上，且至少处于原点附近，式中C是正常数。随着∣∣x∣∣→∞，上述封闭曲面可扩展为整个状态空间。如果C1＜C2，则超曲面V（x）＝C1完全处于超曲面V（x）＝C2的内部。

对于给定的系统，若可求得正定的纯量函数V（x），并使其沿轨迹对时间的导数总为负值，则随着时间的增加，V（x）将取越来越小的C值。随着时间的进一步增长，最终V（x）变为零，而x也趋于零。这意味着，状态空间的原点是渐近稳定的。李雅普诺夫主稳定性定理就是前述事实的普遍化，它给出了渐近稳定的充要条件。该定理阐述如下。

定理9-4 （李雅普诺夫，皮尔希德斯基，巴巴辛，克拉索夫斯基） 考虑如下非线性系统

式中

f（0，t）≡0， 对所有t≥t0

如果存在一个具有连续一阶偏导数的纯量函数V（x，t），且满足以下条件：

a.V（x，t）正定；

b.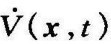负定。

则在原点处的平衡状态是（一致）渐近稳定的。

进一步地，若∣∣x∣∣→∞，V（x，t）∞，则在原点处的平衡状态是大范围一致渐近稳定的。

例9-34 考虑如下非线性系统

显然原点（x1＝0，x2＝0）是惟一的平衡状态。试确定其稳定性。

解 如果定义一个正定纯量函数，则沿任一轨迹，有

是负定的，这说明V（x）沿任一轨迹连续地减小，因此V（x）是一个李雅普诺夫函数。由于V（x）随x偏离平衡状态趋于无穷而变为无穷，则按照定理9-4，该系统在原点处的平衡状态是大范围渐近稳定的。

注意，若使V（x）取一系列的常值0，C1，C2，⋯，（0＜C1＜C2＜⋯），则V（x）＝0对应于状态平面的原点，而V（x）＝C1，V（x）＝C2，⋯，描述了包围状态平面原点的互不相交的一簇圆，如图9-26所示。还应注意，由于V（x）在径向是无界的，即随着∣∣x∣∣→∞，V（x）→∞，所以这一簇圆可扩展到整个状态平面。

由于圆V（x）＝Ck完全处在V（x）＝Ck＋1的内部，所以典型轨迹从外向里通过V圆的边界。因此李雅普诺夫函数的几何意义可阐述如下V（x）表示状态x到状态空间原点距离的一种度量。如果原点与瞬时状态x（t）之间的距离随t的增加而连续地减小（即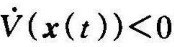），则x（t）→0。

图9-26 常数V圆和典型轨迹

定理9-4是李雅普诺夫第二法的基本定理，下面对这一重要定理作几点说明。

a.这里仅给出了充分条件，也就是说，如果构造出了李雅普诺夫函数V（x，t），那么系统是渐近稳定的。但如果找不到这样的李雅普诺夫函数，则不能给出任何结论，例如不能据此说该系统是不稳定的。

b.对于渐近稳定的平衡状态，则李雅普诺夫函数必存在。

c.对于非线性系统，通过构造某个具体的李雅普诺夫函数，可以证明系统在某个稳定域内是渐近稳定的，但这并不意味着稳定域外的运动是不稳定的。对于线性系统，如果存在渐近稳定的平衡状态，则它必定是大范围渐近稳定的。

d.这里给出的稳定性定理，既适合于线性系统、非线性系统，也适合于定常系统、时变系统，具有极其一般的普遍意义。

显然，定理9-4仍有一些限制条件，比如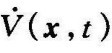必须是负定函数。如果在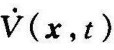上附加一个限制条件，即除了原点以外，沿任一轨迹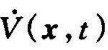均不恒等于零，则要求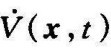负定的条件可用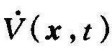取负半定的条件来代替。

定理9-5 （克拉索夫斯基，巴巴辛） 考虑如下非线性系统

式中

f（0，t）≡0， 对所有t≥t0

若存在具有连续一阶偏导数的纯量函数V（x，t），且满足以下条件：

a.V（x，t）是正定的；

b.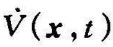是负半定的；

c.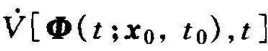对于任意t0和任意x0≠0，在t≥t0时，不恒等于零，其中的Φ（t；x0，t0）表示在t0时从x0出发的轨迹或解，则在系统原点处的平衡状态是大范围渐近稳定的。

注意，若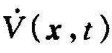不是负定的，而只是负半定的，则典型点的轨迹可能与某个特定曲面V（x，t）＝C相切，然而由于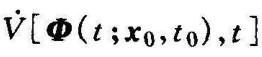对任意t0和任意x0≠0，在t≥t0时不恒等于零，所以典型点就不可能保持在切点处（在这点上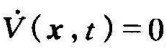，），因而必然要运动到原点。

②关于稳定性。

然而，如果存在一个正定的纯量函数V（x，t），使得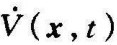始终为零，则系统可以保持在一个极限环上。在这种情况下，原点处的平衡状态称为在李雅普诺夫意义下是稳定的。

定理9-6（李雅普诺夫） 考虑如下非线性系统

式中

f（0，t）≡0， 对所有t≥t0

若存在具有连续一阶偏导数的纯量函数V（x，t），且满足以下条件：

a.V（x，t）是正定的；

b.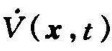是负半定的；

c.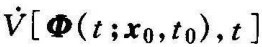对于任意t0和任意x0≠0，在t≥t0时，均恒等于零，其中的Φ（t；x0，t0），表示在t0时从x0出发的轨迹或解，则在系统原点处的平衡状态是李雅普诺夫意义下的大范围渐近稳定的。

③关于不稳定性

如果系统平衡状态x＝0是不稳定的，则存在纯量函数W（x，t），可用其确定平衡状态的不稳定性。下面介绍不稳定性定理。

定理9-7（李雅普诺夫） 考虑如下非线性系统

式中

f（0,1）≡0， 对所有t≥to

若存在一个纯量函数W（x，t），具有连续的一阶偏导数，且满足下列条件：

a.W（x，t）在原点附近的某一邻域内是正定的；

b.在同样的邻域内是正定的。则原点处的平衡状态是不稳定的。

（3）线性系统的稳定性与非线性系统的稳定性比较

在线性定常系统中，若平衡状态是局部渐近稳定的，则它是大范围渐近稳定的，然而在非线性系统中，不是大范围渐近稳定的平衡状态可能是局部渐近稳定的。因此，线性定常系统平衡状态的渐近稳定性的含义和非线性系统的含义完全不同。

如果要检验非线性系统平衡状态的渐近稳定性，则非线性系统的线性化模型稳定性分析远远不够，必须研究没有线性化的非线性系统。有几种基于李雅普诺夫第二法的方法可达到这一目的，包括用于判断非线性系统渐近稳定性充分条件的克拉索夫斯基方法、用于构成非线性系统李雅普诺夫函数的阿塞尔曼法、Schultz-Gibson变量梯度法、用于某些非线性控制系统稳定性分析的鲁里叶（Lure’）法，以及用于构成吸引域的波波夫方法等。下面介绍几种常用的方法。

①阿塞尔曼法。

设系统的状态方程为

式中，b＝[1 0 ⋯0 0]T，f（xi）为单值非线性函数，f（0）＝0，xi为x1，x2，⋯， xn中的任意一个变量，展开式（9-180）有

由于x＝0时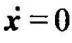，说明状态空间的原点是平衡点。阿塞尔曼法的思想是用线性函数代替非线性函数，即令f（xi）＝kxi，将系统线性化以后，就可用比较容易构造李雅普诺夫函数V（x），然后将此函数当作非线性系统的备选李雅普诺夫函数。如果其导数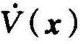在区间k1≤k≤k2是负定的，则可以得出结论：当非线性系统中的非线性元件满足条件k1xi≤kxi≤k2xi时，非线性系统在x＝0处其平衡状态是大范围渐近稳定的，如图9-27所示。

图9-27 非线性特性

例9-35 设非线性系统的动态方程为

其中，f（x）为非线性函数，试分析其稳定性。

解令x1＝x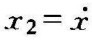，，则系统的状态方程为

其结构图如图9-28所示。

图9-28 非线性系统结构图

a.假设非线性元件的输入输出特性如图9-29所示，它可以用一条斜率为k＝2的直线来近似，即

u＝f（x1）≈2x1

图9-29 非线性元件的输入输出特性

于是，线性化以后的系统状态方程为

b.构造李雅普诺夫函数。取二次型李雅普诺夫备选函数为

c.对线性化系统求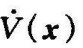

设有如下的简单形式

则比较式（9-184）和式（9-183）可得

由此解得，p11＝5/4，p12＝1/4，p22＝3/8。

d.将上述结果代入式（9-183），得

可证明它是正定的，这说明线性化系统（9-182）在平衡点是渐近稳定的。

e.将式（9-185）看成非线性系统（9-181）的李雅普诺夫备选函数，则

式（9-181）代入式（9-186），可得

根据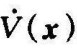负定的要求，应有

由此解出

这就是说，式（9-184）是非线性系统（9-181）的李雅普诺夫函数。只要非线性特性u＝f（x1）在图的阴影区内，非线性系统的V（x）正定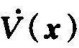，负定，系统在平衡点处是大范围渐近稳定的。

阿塞尔曼方法简单实用，但是必须指出，在有些场合，即使线性化之后的系统在所有的k下是稳定的，非线性系统也不一定是大范围稳定的。

②克拉索夫斯基方法。

克拉索夫斯基方法给出了非线性系统平衡状态渐近稳定的充分条件。克拉索夫斯基方法的基本思想是不用状态变量，而是用其导数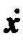来构造李雅普诺夫函数。不失一般性，可认为状态空间的原点是系统的平衡状态。

定理9-8（克拉索夫斯基定理） 考虑如下非线性系统

式中，x为n维状态向量，f（x）为x1，x2，，xn的非线性n维向量函数，假定f（0）＝0，且f（x）对xi可微（i＝1，2，⋯，n）。(www.xing528.com)

该系统的雅可比矩阵定义为

又定义

式中，F（x）是雅可比矩阵，FT（x）是F（x）的转置矩阵，为实对称矩阵。如果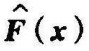是负定的，则平衡状态x＝0是渐近稳定的。该系统的李雅普诺夫函数为

V（x）＝f T（x）f（x）

此外，若随着x∣∣→∞，f T（x）f（x）→∞，则平衡状态是大范围渐近稳定的。

证由于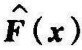是负定的，所以除x＝0外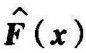，的行列式处处不为零。因而，在整个状态空间中，除x＝0这一点外，没有其他平衡状态，即在x≠0时，f（x）≠0。因为f（0）＝0，在x≠0时，f（x）0，且V（x）＝f T（x）f（x），所以V（x）是正定的。

注意到

从而

因为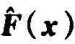是负定的，所以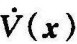也是负定的。因此，V（x）是一个李雅普诺夫函数，所以原点是渐近稳定的。如果随着∣∣x∣∣→∞，V（x）＝fT（x）f（x）→∞，则根据定理9-4可知，平衡状态是大范围渐近稳定的。

注意，克拉索夫斯基定理与通常的线性方法不同，它不局限于稍稍偏离平衡状态的情况。V（x）和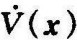以f（x）或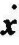的形式而不是以x的形式表示。

前面所述的定理对于非线性系统给出了大范围渐近稳定性的充分条件，对线性系统则给出了充要条件。非线性系统的平衡状态即使不满足上述定理所要求的条件，也可能是稳定的。因此，在应用克拉索夫斯基定理时，必须十分小心，以防止对给定的非线性系统平衡状态的稳定性分析做出错误的结论。

例9-36 考虑具有两个非线性因素的二阶系统

假设f1（0）＝f2（0）＝0，f1（x1）和f2（x2）是实函数且可微。又假定当∣∣x∣∣→∞时， [f1（x1）＋f2（x2）]2＋（x1＋ax2）2→∞。试确定使平衡状态x＝0渐近稳定的充分条件。

解在该系统中，F（x）为

式中

于是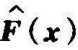为

由克拉索夫斯基定理可知，如果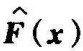是负定的，则所考虑系统的平衡状态x＝0是大范围渐近稳定的。因此，若

则平衡状态xe＝0是大范围渐近稳定的。

这两个条件是渐近稳定性的充分条件。显然，由于稳定性条件完全与非线性f1（x）和f2（x）的实际形式无关，所以上述限制条件是不适当的。

（4）线性定常系统的李雅普诺夫稳定性分析

前已指出，李雅普诺夫第二法不仅对非线性系统，而且对线性定常系统、线性时变系统，以及线性离散系统等均完全适用。

利用李雅普诺夫第二法对线性系统进行分析，有如下几个特点：

①都是充要条件，而非仅充分条件；

②渐近稳定性等价于李雅普诺夫方程的存在性；

③渐近稳定时，必存在二次型李雅普诺夫函数V（x）＝x TPx及；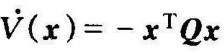

④对于线性自治系统，当系统矩阵A非奇异时，仅有惟一平衡点，即原点xe＝0；

⑤渐近稳定就是大范围渐近稳定，两者完全等价。

众所周知，对于线性定常系统，其渐近稳定性的判别方法很多。例如，对于连续时间定常系统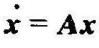，渐近稳定的充要条件是：A的所有特征值均有负实部，或者相应的特征方程∣sI－A∣＝sn＋a1sn－1＋⋯＋an－1s＋an＝0的根具有负实部。但为了避开困难的特征值计算，如劳斯-赫尔维茨稳定性判据通过判断特征多项式的系数来直接判定稳定性，奈奎斯特稳定性判据根据开环频率特性来判断闭环系统的稳定性。这里将介绍的线性系统的李雅普诺夫稳定性方法，是一种代数方法，不要求把特征多项式进行因式分解，而且可进一步应用于求解某些最优控制问题。

考虑如下线性定常自治系统

式中，x∈Rn，A∈Rn×n。假设A为非奇异矩阵，则有惟一的平衡状态xe＝0，其平衡状态的稳定性很容易通过李雅普诺夫第二法进行研究。

对于式（9-187）的系统，选取如下二次型李雅普诺夫函数，即

V（x）＝x TPx

式中P为正定的实对称矩阵。V（x）沿任一轨迹的时间导数为

由于V（x）取为正定，对于渐近稳定性，要求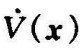为负定的，因此必须有

式中

﹣Q＝ATP＋PA

为正定矩阵。因此，对于式（9-187）的系统，其渐近稳定的充要条件是Q正定。为了判断n×n维矩阵的正定性，可采用赛尔维斯特准则，即矩阵为正定的充要条件是矩阵的所有主子行列式均为正值。

在判别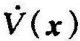时，方便的方法，不是先指定一个正定矩阵P，然后检查Q是否也是正定的，而是先指定一个正定的矩阵Q，然后检查由

ATP＋PA＝﹣Q

确定的P是否也是正定的。这可归纳为如下定理。

定理9-9 线性定常系统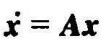在平衡点xe＝0处渐近稳定的充要条件是：对于任意Q＞0，存在P＞0满足如下李雅普诺夫方程

ATP＋PA＝﹣Q

这里P，Q均为实对称矩阵。此时，李雅普诺夫函数为

现对该定理作以下几点说明：

①如果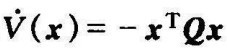沿任一条轨迹不恒等于零，则Q可取正半定矩阵；

②如果取任意的正定矩阵Q，或者如果沿任一轨迹不恒等于零时取任意的正半定矩阵Q，并求解矩阵方程

ATP＋PA＝﹣Q

以确定P，则对于在平衡点xe＝0处的渐近稳定性，P为正定是充要条件；

③只要选择的矩阵Q为正定的（或根据情况选为正半定的），则最终的判定结果将与矩阵Q的不同选择无关。通常取Q＝I。

例9-37 设二阶线性定常系统的状态方程为

显然，平衡状态是原点。试确定该系统的稳定性。

解 不妨取李雅普诺夫函数为

V（x）＝x TPx

此时实对称矩阵P可由下式确定

ATP＋PA＝﹣I

上式可写为

将矩阵方程展开，可得联立方程组为

从方程组中解出p11，p12，p22，可得

为了检验P的正定性，先来校核各主子行列式

显然，P是正定的。因此，在原点处的平衡状态是大范围渐近稳定的，且李雅普诺夫函数为

且

例9-38试确定如图9-30所示系统的增益K的稳定范围。

图9-30 控制系统框图

解 容易推得系统的状态方程为

在确定K的稳定范围时，假设输入u为零。于是上式可写为

由式（9-188）到式（9-190）可发现，原点是平衡状态。假设取正半定的实对称矩阵Q为

由于除原点外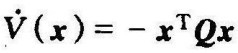不恒等于零，因此可选上式的Q。为了证实这一点，注意

取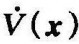恒等于零，意味着x3也恒等于零。如果x3恒等于零，x1也必恒等于零，因为由式（9-190）可得

﹣Kx1＝0

如果x1恒等于零，x2也恒等于零。因为由式（9-188）可得

0＝x2

于是只在原点处才恒等于零。因此，为了分析稳定性，可采用由式（9-190）定义的矩阵Q。

现在求解如下李雅普诺夫方程

ATP＋PA＝﹣Q

它可重写为

对P的各元素求解，可得

为使P成为正定矩阵，其充要条件为

12－2K＞0 和K＞0

或

0＜K ＜6

因此，当0＜K＜6时，系统在李雅普诺夫意义下是稳定的，也就是说，原点是大范围渐近稳定的。

线性定常离散系统渐近稳定的判别。

设系统状态方程为

x（k＋1）＝Gx（k）（9-191）

式中，G为非奇异矩阵，原点是平衡状态。设取如下正定二次型函数

V[x（k）]＝x T（k）Px（k）（9-192）

以代替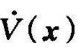，计算△V[x（k）]有

△V[x（k）]＝x T（k＋1）Px（k＋1）－x T（k）Px（k）＝[Gx（k）]TP[Gx（k）]－x T（k）Px（k）＝x T（k）[GTPG－P]x（k）（9-193）

令

GTPG －P＝﹣Q（9-194）

式（9-194）称为离散的李雅普诺夫代数方程，于是

△[x（k）]＝﹣x T（k）Qx（k）

于是得到如下定理：

定理9-10 离散系统x（k＋1）＝Gx（k）渐近稳定的充要条件是，给定任一正定实对称矩阵Q，存在一个正定实对称矩阵P，使式（9-194）成立。x T（k）Px（k）是系统的一个李雅普诺夫函数。通常可取Q＝I。

如果△V[x（k）]沿任意一个解的序列不恒为零，Q也可以取为半正定矩阵。