李雅普诺夫稳定性问题的意义

对于一个给定的控制系统，稳定性分析通常是最重要的。如果系统是线性定常的，那么有许多稳定性判据，如劳斯-赫尔维茨稳定性判据和奈奎斯特稳定性判据等可资利用。然而，如果系统是非线性的，或是线性时变的，则上述稳定性判据就将不再适用。

李雅普诺夫于1892年首先研究了一般微分方程的稳定性问题，提出了两种方法，称为李雅普诺夫第一法（间接法）和李雅普诺夫第二法（直接法），用于确定由常微分方程描述的动力学系统的稳定性。其中，第二法是确定非线性系统和线性时变系统的最一般的方法。当然，这种方法也可适用于线性定常系统的稳定性分析。

（1）平衡状态、给定运动与扰动方程的原点

考虑如下非线性系统

式中x为n维状态向量，f（x，t）是变量x1，x2，⋯，xn和t的n维向量函数。假设在给定的初始条件下，式（9-178）有惟一解Φ（t；x0，t0），当t＝t0时，x＝x0，于是Φ（t；x0，t0）＝x0

在式（9-178）的系统中，若总存在

f（xe，t）＝0，对所有t（9-179）

则称xe为系统的平衡状态或平衡点。如果系统是线性定常的，也就是说f（x，t）＝Ax，则当A为非奇异矩阵时，系统存在一个惟一的平衡状态；当A为奇异矩阵时，系统将存在无穷多个平衡状态。对于非线性系统，可有一个或多个平衡状态，这些状态对应于系统的常值解（对所有t，总存在x＝xe）。平衡状态的确定不包括式（9-178）的系统微分方程的解，只涉及式（9-179）的解。

任意一个孤立的平衡状态（即彼此孤立的平衡状态）或给定运动x＝g（t）都可通过坐标变换，统一化为扰动方程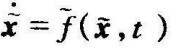之坐标原点，即f（0，t）＝0或xe＝0。在本节中，除非特别申明，这里将仅讨论扰动方程关于原点（xe＝0）处之平衡状态的稳定性问题。这种“原点稳定性问题”由于使问题得到极大简化，而不会丧失一般性，从而为稳定性理论的建立奠定了坚实的基础，这是李雅普诺夫的一个重要贡献。

（2）李雅普诺夫意义下的稳定性定义

下面首先给出李雅普诺夫意义下的稳定性定义，然后回顾某些必要的数学基础，以便在下一小节具体给出李雅普诺夫稳定性定理。

定义9-1（李雅普诺夫意义下的稳定） 设系统

的平衡状态xe＝0的H邻域为

∣∣x－xe∣∣≤H

其中，H＞0，∣∣∣∣为向量的L2范数或欧几里德范数，即

类似地，也可以相应定义球域S（ε）和S（δ）。

在H邻域内，对于任意给定的0＜ε＜H。

①如果对应于每一个S（ε），存在一个S（δ），使得当t趋于无穷时，始于S（δ）的轨迹不脱离S（ε），则式（9-178）系统之平衡状态xe＝0称为在李雅普诺夫意义下是稳定的。一般地，实数δ与ε有关，通常也与t0有关。如果δ与t0无关，则此时平衡状态xe＝0称为一致稳定的平衡状态。

以上定义意味着：首先选择一个域S（ε），对应于每一个S（ε），必存在一个域S（δ），使得当t趋于无穷时，始于S（δ）的轨迹总不脱离域S（ε）。

②如果平衡状态xe＝0，在李雅普诺夫意义下是稳定的，并且始于域S（δ）的任一条轨迹，当时间t趋于无穷时，都不脱离S（ε），且收敛于xe＝0，则称式（9-178）系统之平衡状态xe＝0为渐近稳定的，其中球域S（δ）被称为平衡状态xe＝0的吸引域。

实际上，渐近稳定性比纯稳定性更重要。考虑到非线性系统的渐近稳定性是一个局部概念，所以简单地确定渐近稳定性并不意味着系统能正常工作，通常有必要确定渐近稳定性的最大范围或吸引域。它是产生渐近稳定轨迹的那部分状态空间。换句话说，发生于吸引域内的每一个轨迹都是渐近稳定的。

③对所有的状态（状态空间中的所有点），如果由这些状态出发的轨迹都保持渐近稳定性，则平衡状态xe＝0称为大范围渐近稳定。或者说，如果式（9-178）系统的平衡状态xe＝0渐近稳定的吸引域为整个状态空间，则称此时系统的平衡状态xe＝0为大范围渐近稳定的。显然，大范围渐近稳定的必要条件是在整个状态空间中只有一个平衡状态。

在控制工程问题中，总希望系统具有大范围渐近稳定的特性。如果平衡状态不是大范围渐近稳定的，那么问题就转化为确定渐近稳定的最大范围或吸引域，这通常非常困难。然而，对所有的实际问题，如能确定一个足够大的渐近稳定的吸引域，以致扰动不会超过它就可以了。

④如果对于某个实数ε＞0和任一个实数δ＞0，不管这两个实数多么小，在S（δ）内总存在一个状态x0，使得始于这一状态的轨迹最终会脱离开S（ε），那么平衡状态xe＝0称为不稳定的。

图9-25（a）、（b）和（c）分别表示平衡状态及对应于稳定性、渐近稳定性和不稳定性的典型轨迹。在图9-24（a）、（b）和（c）中，域S（δ）制约着初始状态x0，而域S（e）是起始于x0的轨迹的边界。

图9-25 平衡状态的稳定性分析(www.xing528.com)

注意，由于上述定义不能详细地说明可容许初始条件的精确吸引域，因而除非S（ε）对应于整个状态平面，否则这些定义只能应用于平衡状态的邻域。

此外，在图9-25（c）中，轨迹离开了S（ε），这说明平衡状态是不稳定的。然而却不能说明轨迹将趋于无穷远处，这是因为轨迹还可能趋于在S（ε）外的某个极限环（如果线性定常系统是不稳定的，则在不稳定平衡状态附近出发的轨迹将趋于无穷远。但在非线性系统中，这一结论并不一定正确）。

对于线性系统，渐近稳定等价于大范围渐近稳定。但对于非线性系统，一般只考虑吸引区为有限的定范围的渐近稳定。

最后必须指出，在经典控制理论中已经学过的稳定性概念，它与李雅普诺夫意义下的稳定性概念是有一定的区别，例如，在经典控制理论中只有渐近稳定的系统才称为稳定的系统。在李雅普诺夫意义下是稳定的但却不是渐近稳定的系统，则叫做不稳定系统。两者的区别与联系如表9-2所示。

表9-2

（3）预备知识

在李雅普诺夫稳定性理论中，能量函数是一个重要的基本概念。该概念在数学上可以采用一类二次型函数来描述，下面简要介绍其基本知识。

①纯量函数的正定性如果对所有在域Ω中的非零状态x≠0，有V（x）＞0，且在x＝0处有V（0）＝0，则在域Ω（域Ω包含状态空间的原点）内的纯量函数V（x）称为正定函数。例如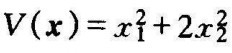是正定的。

如果时变函数V（x，t）由一个定常的正定函数作为下限，即存在一个正定函数V（x），使得

V（x，t）＞V（x）， 对所有t≥t0

V（0，t）＝0， 对所有t≥t0

则称时变函数V（x，t）在域Ω（Ω包含状态空间原点）内是正定的。

②纯量函数的负定性如果﹣V（x）是正定函数，则纯量函数V（x）称为负定函数。例如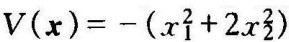是负定的。

③纯量函数的正半定性如果纯量函数V（x）除了原点以及某些状态等于零外，在域Ω内的所有状态都是正定的，则V（x）称为正半定纯量函数。例如V（x）＝（x1＋x2）2是正半定的。

④纯量函数的负半定性如果﹣V（x）是正半定函数，则纯量函数V（x）称为负半定函数。例如V（x）＝﹣（x1＋2x2）2是负半定的。

⑤纯量函数的不定性如果在域Ω内，不论域Ω多么小，V（x）既可为正值，也可为负值时，纯量函数V（x）称为不定的纯量函数。例如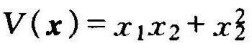是不定的。

⑥二次型 建立在李雅普诺夫第二法基础上的稳定性分析中，有一类纯量函数起着很重要的作用，即二次型函数。例如

注意，这里的x为实向量，P为实对称矩阵。二次型V（x）的正定性可用赛尔维斯特准则判断。该准则指出，二次型V（x）为正定的充要条件是矩阵P的所有主子行列式均为正值，即

如果P是奇异矩阵，且它的所有主子行列式均非负，则V（x）＝x TPx是正半定的。

如果﹣V（x）是正定的，则V（x）是负定的。同样，如果﹣V（x）是正半定的，则V（x）是负半定的。

例9-33 试证明下列二次型是正定的

证二次型V（x）可写为

利用赛尔维斯特准则，可得

因为矩阵P的所有主子行列式均为正值，所以V（x）是正定的。