状态反馈和极点配置的优化方案

以下讨论利用状态反馈进行极点配置的方法，这里仅研究控制输入为标量的情况，介绍两种确定状态反馈增益矩阵的方法。

（1）问题的提法

给定单输入单输出线性定常被控系统

式中，x（t）∈Rn，u（t）∈R1，A∈Rn×n，B∈Rn×1。

选取线性反馈控制律为

u＝υ－Kx（9-123）

式中K∈R1×n为状态反馈增益矩阵或线性状态反馈矩阵。在下面的分析中，假设u不受约束。

图9-15（a）给出了由式（9-122）所定义的系统。因为没有将状态x反馈到控制输入u中，所以这是一个开环控制系统。图9-15（b）给出了具有状态反馈的系统。因为将状态x反馈到了控制输入u中，所以这是一个闭环反馈控制系统。

图9-15 开环与闭环控制系统

将式（9-123）代入式（9-122），得到

由此可见，系统的响应特性将由闭环系统矩阵A－BK的特征值决定。如果矩阵K选取适当，则可使矩阵A－BK构成一个渐近稳定矩阵。矩阵A－BK的特征值即为闭环系统的极点，这种使闭环系统的极点任意配置到所期望位置的问题，称之为极点配置问题。

下面讨论极点配置条件。将证明，当且仅当给定的系统是状态完全可控时，该系统的任意极点配置才是可能的。

（2）可配置条件

考虑由式（9-122）定义的线性定常系统。假设控制输入u的幅值是无约束的。如果选取控制规律为

u＝υ－Kx

式中K为线性状态反馈矩阵。

现在考虑极点的可配置条件，即如下的极点配置定理。

定理9-1（极点配置定理） 线性定常系统可通过线性状态反馈任意地配置其全部极点的充要条件是，此被控系统状态完全可控。

证 这里只给出单输入单输出系统时的证明。但要着重指出的是，这一定理对多变量系统也是完全成立的。

①充分性。即已知被控系统状态完全可控（这意味着由式（9-125）给出的矩阵Q有逆），则矩阵A的所有特征值可任意配置。

如果式（9-122）给出的系统状态完全可控，一定存在非奇异变换，使其变换为可控标准形。定义非奇异线性变换矩阵P为

P＝QW（9-124）

其中Q为可控性矩阵，即

式中ai为如下特征多项式的系数。

∣sI－A ∣＝sn＋a1sn－1＋⋯＋an－1s＋an

定义一个新的状态向量

如果可控性矩阵Q的秩为n（即系统是状态完全可控的），则矩阵Q 的逆存在，并且可将式（9-122）改写为

其中

式（9-127）为可控标准形。这样，如果系统是状态完全可控的，且利用由式（9-124）给出的变换矩阵P，使状态向量x变换为状态向量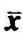，则可将式（9-122）变换为可控标准形。

选取一组期望的特征值为μ1，μ2，⋯，μn，则期望的特征方程为

设

由于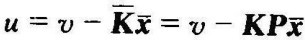，从而由式（9-126），此时该系统的状态方程为

相应的特征方程为

事实上，因为非奇异线性变换不改变系统的特征值，当利用u＝υ－Kx作为控制输入时，相应的特征方程与式（9-130）的特征方程相同。

对于上述可控标准形的系统特征方程，由式（9-126）和式（9-127），可得

这是具有线性状态反馈的闭环系统的特征方程，它一定与式（9-128）的期望特征方程相等。通过使s的同次幂系数相等，可得

对δi求解上述方程组，并将其代入式（9-130），可得

因此，如果系统是状态完全可控的，则通过对应于式（9-131）所选取的矩阵K，可任意配置所有的特征值。

②必要性。即已知闭环系统可任意配置极点，则被控系统状态完全可控。

现利用反证法证明。先证明如下命题：如果系统不是状态完全可控的，则矩阵A－BK的特征值不可能由线性状态反馈来控制。

假设式（9-122）的系统状态不可控，则其可控性矩阵的秩小于n，即

rank[B AB ⋯An－1B]＝q＜n

这意味着，必有状态变量与控制u无关，因此，不可能实现如式（9-123）所示的全状态反馈，于是不可控子系统的特征值就不能任意配置。所以，为了任意配置矩阵A－BK的特征值，此时系统必须是状态完全可控的。必要性得证。

（3）极点配置的算法

现在考虑单输入单输出系统极点配置的算法。

给定线性定常系统

若线性反馈控制律为 u＝υ－Kx

则可由下列步骤确定使A －BK 的特征值为μ1，μ2，⋯，μn（即闭环系统的期望极点值）的线性反馈矩阵K （如果μi是一个复数特征值，则其共轭必定也是A－BK的特征值）。

①考察系统的可控性条件。如果系统是状态完全可控的，则可按下列步骤继续。

②计算系统矩阵A的特征多项式

det（sI－A）＝∣sI－A∣＝sn＋a1sn－1＋⋯＋an－1s＋an

确定a1，a2，⋯，an的值。

③确定将系统状态方程变换为可控标准形的变换矩阵P。若给定的状态方程已是可控标准形，那么P＝I。此时无需再写出系统的可控标准形状态方程。非奇异线性变换矩阵P可由式（9-124）给出，即

P＝QW

式中Q，W由式（9-125）定义。

④利用给定的期望闭环极点，可写出期望的特征多项式为

并确定出的值。

⑤此时的状态反馈增益矩阵K为

例9-28 考虑如下线性定常系统

式中

利用状态反馈控制u＝υ－Kx，希望该系统的闭环极点为s＝﹣2±j4和s＝﹣10。试确定状态反馈增益矩阵K。

解 首先需检验该系统的可控性矩阵。由于可控性矩阵为

所以得出detQ＝﹣1。因此，rankQ＝3。因而该系统是状态完全可控的，可任意配置极点。

下面来求解这个问题，并介绍两种求解方法。(www.xing528.com)

方法1 第一种方法是利用式（9-131）。该系统的特征方程为

因此

a1＝6，a2＝5，a3＝1

期望的特征方程为

因此

参照式（9-131），可得

K＝[200－1 60－5 14－6]＝[199 55 8]

方法2 设期望的状态反馈增益矩阵为

K＝[k1 k2 k3]

并使[sI－A＋BK]和期望的特征多项式相等，可得

因此

从中可得

或

K＝[199 55 8]

显然，这两种方法所得到的反馈增益矩阵K是相同的。正如所期望的那样，使用状态反馈方法可将闭环极点配置在s＝﹣2±j4和s＝﹣10处。

应当注意，如果系统的阶次n等于或大于4，则推荐使用方法1，因为所有的矩阵计算都可由计算机实现。如果使用方法2，由于计算机不能处理含有未知参数k1，k2，…，kn的特征方程，因此必须进行手工计算。

对于一个给定的系统，矩阵K依赖于选择期望闭环极点的位置（这决定了响应速度与阻尼），这一点很重要。注意，所期望的闭环极点或所期望状态方程的选择是在误差向量的快速性和干扰以及测量噪声的灵敏性之间的一种折中。也就是说，如果加快误差响应速度，则干扰和测量噪声的影响通常也随之增大。如果系统是二阶的，那么系统的动态特性（响应特性）正好与系统期望的闭环极点和零点的位置联系起来。对于更高阶的系统，所期望的闭环极点位置不能和系统的动态特性（响应特性）联系起来。必须指出的是，对单输入/单输出系统，采用状态反馈并不能改变系统的零点。由于系统的零点对系统的动态性能影响很大，在选择希望配置的闭环系统极点时，必须充分考虑闭环零点的影响，这些基本概念在经典控制理论中已经研究过。因此，在决定给定系统的状态反馈增益矩阵K时，最好通过计算机仿真来检验系统在几种不同矩阵（基于几种不同的所期望的特征方程）下的响应特性，并且选出使系统总体性能最好的矩阵K。下面以一个自动测试系统的闭环极点配置为例，说明通过选择闭环零点来满足一定的时域性能指标要求。

例9-29 自动测试系统。

某自动测试系统的状态空间表达式如下

设计目标为，其闭环系统的阶跃响应满足①调整时间ts小于2s；②超调量σp小于4％。

解 采用状态反馈的方法，有

u＝﹣Kx＝﹣[K1 K2 K3]x

利用第3章二阶系统动态系统参数值之间关系，可得近似值

由此可得

ζ＞0.72， ωn＞2.8

闭环特征多项式det（sI－A－KB）为

将bK3看成一个参数，且令K1＝1，可将式（9-132）写成

选择零点s＝﹣4±j2，可得期望分子多项式为s2＋8s＋20。比较相应的系数可得

由此可得K2＝0.35，K3＝0.35。选择bK3＝12，可满足动态特性要求。最终的状态反馈矩阵K和增益b为

b＝240.00，K＝[1.00 0.35 0.05]

最终的系统阶跃响应如图9-16所示，可得调整时间ts为1.8s，超调量σp为3％，满足设计要求。

图9-16 自动测试系统的闭环阶跃响应

（4）利用Matlab求解极点配置问题

用Matlab易于解极点配置问题。现在我们来求解例9-27中讨论的同样问题。系统方程为

式中

采用状态反馈控制u＝﹣Kx，希望系统的闭环极点为s＝μi（i＝1，2，3），其中

μ1＝﹣2＋j4，μ2＝﹣2－j4，μ3＝﹣10

现求所需的状态反馈增益矩阵K。

如果在设计状态反馈控制矩阵K时采用变换矩阵P，则必须求特征方程∣sI－A∣＝0的系数a1，a2和a3。这可利用Matlab函数poly.m

P＝poly（A）

来实现。例如，对本例

则a1＝a1＝P（2），a2＝a2＝P（3），a3＝a3＝P（4）。

为了得到变换矩阵P，首先将矩阵Q和W输入计算机，其中

然后可以很容易地采用Matlab完成Q和W相乘。

其次，再求期望的特征方程。可定义矩阵J，使得

从而可利用如下poly（J）命令来完成，即

因此，有

即对于，可采用aai。

故状态反馈增益矩阵K可由下式确定

Matlab命令为

K＝[aa3－a3aa2－a2aa1－a1]*（inv（P））

采用变换矩阵P求解例9-27的Matlab程序如Matlab Program9-5所示。

Matlab的控制系统工具箱还提供了几个函数，可以直接用于极点配置的状态反馈矩阵计算。

①基于Ackermann的极点配置算法，这种方法中的状态反馈矩阵按式（9-133）计算

K＝﹣[0 0 ⋯0 1]w﹣1Φ（A）（9-133）

式中，W由式（9-125）定义，Φ(A）＝An＋a1An﹣1＋⋯＋an﹣1A＋anI，ai（i＝1，2，⋯， n）是特征多项式的系数。

相应的matlab函数为acker.m

K＝acker（A，B，P）

其中，A，B为系统矩阵，P为包含期望极点位置的向量，K为返回的状态反馈矩阵。

②place函数。调用方式为

K＝place（A，B，P）

式中各参数的意义同函数acker。