线性连续系统的可控性分析

（1）可控性定义

考虑线性连续时间系统

其中，x（t）∈Rn，u（t）∈R1，A∈Rn×n，B∈Rn×1（单输入），且初始条件为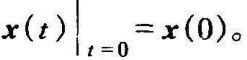

如果施加一个无约束的控制信号，在有限的时间间隔t0≤t≤t1内，能够使初始状态转移到任一终止状态，则称由式（9-90）描述的系统在t＝t0时为状态（完全）可控的。如果每一个状态都可控，则称该系统为状态（完全）可控的。

（2）定常系统状态可控性的代数判据

下面推导状态可控的条件。不失一般性，设终止状态为状态空间原点，并设初始时刻为零，即t0＝0。

由上一节的内容可知，式（9-90）的解为

利用状态可控性的定义，可得

或

将e﹣Ar写为A的有限项的形式，即

将式（9-92）代入式（9-91），可得

记

则式（9-91）成为

如果系统是状态可控的，那么给定任一初始状态x（0），都应满足式（9-94）。这就要求n×n维矩阵

Q＝[BABAn－1B]

的秩为n。

由此分析，可将状态可控性的代数判据归纳为：当且仅当n×n维矩阵Q满秩，即

rankQ＝rank[B AB ⋯ An－1B]＝n

时，由式（9-91）确定的系统才是状态可控的。

上述结论也可推广到控制向量u为r维的情况。此时，如果系统的状态方程为

式中，x（t）∈Rn，u（t）∈Rr，A∈Rn×n，B∈Rn×r，那么可以证明，状态可控性的条件为n×nr维矩阵

Q＝[B AB ⋯ An－1B]

的秩为n，或者说其中的n个列向量是线性无关的。通常，我们称矩阵

Q＝[B AB ⋯ An－1B](www.xing528.com)

为可控性矩阵。

例9-20 考虑由下式确定的系统

由于

即Q为奇异阵，所以该系统是状态不可控的。

例9-21 考虑由下式确定的系统

对于该情况

即Q为非奇异，因此系统是状态可控的。

（3）用传递函数矩阵表达的状态可控性条件

状态可控的条件也可用传递函数或传递矩阵描述。状态可控性的充要条件是在传递函数或传递函数矩阵中不出现相约现象。如果发生相约，那么在被约去的模态中，系统不可控。

例9-22 考虑下列传递函数

显然，在此传递函数的分子和分母中存在可约的因子（s＋2.5）（因此少了一阶）。由于有相约因子，所以该系统状态不可控。

当然，将该传递函数写为状态方程，可得到同样的结论。状态方程为

由于

即可控性矩阵[B AB]的秩为1，所以可得到状态不可控的同样结论。

关于利用状态空间标准型判别系统状态完全可控的问题，将在介绍系统标准型之后予以讨论。

（4）输出可控性

在实际的控制系统设计中，需要控制的是输出，而不是系统的状态。对于控制系统的输出，状态可控性既不是必要的，也不是充分的。因此，有必要再定义输出可控性。

考虑下列状态空间表达式所描述的线性定常系统

式中，x∈Rn，u∈Rr，y∈Rm，A∈Rn×n，B∈Rn×r，C∈Rm×n，D∈Rm×r。

如果能找到一个无约束的控制向量u（t），在有限的时间间隔t0≤t≤t1内，使任一给定的初始输出y（t0）转移到任一最终输出y（t1），那么称由式（9-95）和式（9-96）所描述的系统为输出可控的。

可以证明，系统输出可控的充要条件为：当且仅当m×（n＋1）r维输出可控性矩阵

Q′＝[CB CAB CA2B ⋯CAn－1B D]

的秩为m时，由式（9-95）和（9-96）所描述的系统为输出可控的。注意，在式（9-96）中存在Du项，对确定输出可控性是有帮助的。