状态空间描述与传递函数描述的关系

（1）单输入/单输出系统的状态空间描述转换成传递函数

设一单输入/单输出系统的状态空间描述为

式中，x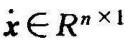，为状态向量及其一阶导数，A∈Rn×n为系统矩阵，B∈Rn×1为系统输入矩阵，C∈R1×n为系统输出矩阵，D为标量，u，y分别为系统的输入和输出信号，均为标量。

设初始条件为零，对式（9-38）进行拉氏变换可得

sX（s）＝AX（s）＋BU（s）

Y（s）＝CX（s）＋DU（s）（9-39）

由式（9-39）可整理得

X（s）＝（sI－A）﹣1BU（s）

将上式代入式（9-39），可得

Y（s）＝C（sI－A）﹣1BU（s）＋DU（s）

由此可得系统的传递函数G（s）为

例9-9 设系统的状态空间描述为

求系统的传递函数。

解由题目可得，状态空间描述的[A ，B，C]分别为

先求（sI－A）﹣1

所以系统的传递函数为

（2）多输入/多输出系统状态空间描述转换成传递函数矩阵

实际的控制系统可能是多输入/多输出系统，如图9-11所示。

图9-11 多输入/多输出系统

图中u1，u2，⋯，ur为系统的输入信号，设有r个。y1，y2，⋯，ym为系统的输出信号，设有m个。x1，x2，⋯，n为系统n个状态变量（设系统是n阶的）。对于图9-11的n阶多输入/多输出系统，其状态空间描述仍为

式中，x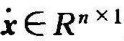，为状态向量及其一阶导数，A∈Rn×n为系统矩阵，B∈Rn×r为系统输入矩阵，C∈Rm×n为系统输出矩阵，D∈Rm×r为系统直接作用矩阵，u，y分别为系统的输入和输出信号向量，u∈Rr×1∈Rm×1，y 。

例9-10 设有如图9-12所示的电枢控制式直流电动机的控制系统。图中，ua为施加于电枢上的控制电压，是系统的控制输入（V）；m L为被拖动的负载转矩（Nm），是系统的扰动输入；θ，ω分别为角位移rad和角速度（rad/s），是系统的两个输出；if为恒定的励磁电流（A）；ea，ia分别为电枢反电势（V）和电枢电流（A）；Ra，La分别为电枢回路的等效电阻（Ω）和等效电感（H）。

图9-12 电枢控制式直流电动机的控制系统

试列出该双输入（ua，m L）双输出（θ，ω）系统的状态空间描述。

解 根据机械旋转运动定律和电路有关定律，图9-12系统的数学模型（微分方程）有

①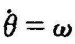

②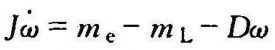(www.xing528.com)

式中，me为电磁转矩；J，D分别为转动惯量及阻尼系数。

③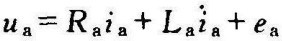

④ea＝k1ω

式中，k1为比例系数。

⑤me＝k2ia

式中，k2为比例系数。

上述①～⑤五个方程，为图9-12系统的原始数学模型，其中包括三个导数项，所以系统是三阶的，包括两个输入和两个输出（见图9-12（b））信号，故系统为一多输入/多输出系统。在式①～⑤中消去中间变量me及ea，可得如下三个一阶微分方程

取θ，ω，ia作为系统的状态变量，即令x1＝θ，x2＝ω，x3＝ia，则式（9-41）的状态空间描述为

再令u1＝ua，u2＝m L，y1＝θ，y2＝ω，将状态方程和输出方程写成矩阵向量形式，可得

上式即为图9-12系统的多输入/多输出（双输入/双输出）系统的状态空间描述。

由于多输入/多输出系统的状态空间描述形式仍为

仅仅不同的是A，B，C，D中的B，C，D与单输入/单输出系统的相应矩阵维数不同。对式（9-42）进行拉氏变换，经整理后，转换结果与式（9-40）形式相同，

G（s）＝C（sI－A）﹣1B＋D（9-43）

只是上式中的A，B，C，D均为矩阵，从而G（s）为矩阵，称为传递函数矩阵。

例9-11 试将例9-10的双输入/双输出系统的状态空间描述，转换成传递函数矩阵G（s）。

解 已知例9-10的状态空间描述的

将上述A，B，C代入式（9-43）可得传递函数矩阵

G（s）＝C（sI－A）﹣1B

上式可改写成

式中，adj（sI－A）为（sI－A）矩阵的伴随矩阵；det（sI－A）为矩阵（sI－A）的行列式。

先求det（sI－A）

再求Cadj（sI－A）B

将式（9-45）、式（9-46）代入式（9-44）得

式（9-47）中，G11（s），G12（s），G21（s），G22（s）都是传递函数。如将式（9-47）改写成

图9-13 传递函数矩阵图

上式用图形表示，如图9-13所示。由图可得，式（9-48）传递函数矩阵G（s）中的四个传递函数分别代表