直流电动机控制系统示例：电枢绕组和转子电路示意图

例9-1 RLC电路的状态空间模型。

图9-1 RLC电路

设有如图9-1所示的RLC电路，根据电工学的定理可以建立RLC电路的动态过程的微分方程为

设ei（t）为输入量，i（t）为输出量，并选择i（t）和∫i（t）dt为状态变量，即设

可推导一阶微分方程组

写成状态方程，有

再设y（t）＝i（t），则相应的输出方程为

再将式（9-5）、式（9-6）写成式（9-1）的形式

其中

例9-2 直流电动机速度控制系统。

控制系统的一个常用的执行器是直流电动机。它可以直接提供旋转运动，可以通过飞轮、鼓和缆的耦合，提供直线运动。图9-2给出了一个电动机电枢绕组电路和带有自由体的转子部分的示意图。

图9-2 直流电动机控制系统示意图

假定对上述对象，有以下物理参数：转子的转动惯量J＝0.01kg·m2/s2，机械系统的阻尼比b＝0.1N·m，电气常数（K＝Ke＝Kt）＝0.01N·m/A，电阻（R）＝1Ω，电感L＝0.5H，系统的输入为电压V，输出轴的位置为θ，假定轴和转子是刚性的。

电动机力矩T与电枢电流i成正比，比例系数为Kt，反电势e与旋转角速度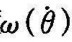成正比，其关系式如下(www.xing528.com)

在SI单位中，Kt（电势常数）等于Ke（电动机常数）。

由图9-2，根据牛顿定律和基尔霍夫定律，可得微分方程组如下

选择轴的角速度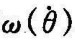和电流i为状态变量，电压为系统输入，角速度ω为系统输出，可得到状态空间表达式如下

状态空间描述与经典控制理论的传递函数描述的最大不同点在于传递函数是对系统的外部描述，又称之为输入输出描述，这种描述不涉及系统内部状况（即状态）的变化情况。而状态空间描述则深入到内部，它既能描述系统的外部行为，又能描述系统的内部行为与性能。

在实际系统中，输入信号将驱动系统状态的变化，而状态的变化将决定系统内部运动与外部的联系。所以描述系统的数学模型-状态空间描述将包括以下两个部分。

①输入对状态的作用关系式，它由状态方程来描述，是一组一阶微分方程式，或者是矩阵向量方程式

上式中，x（t）是状态向量，A，B为系数矩阵，u（t）为输入信号。

②状态变量和输出信号的关系式

y（t）＝Cx（t）（9-10b）

式中，y（t）为输出信号，C为输出矩阵（或向量）。上式称为系统的输出方程式或称之为量测方程。

图9-3给出了状态空间表达式的结构示意图。

图9-3 状态空间表达式结构示意图