使用相平面法分析非线性系统

相平面法绘制的是二阶系统的相轨迹，因此它只能用来分析二阶系统的运动特性。它不仅能分析二阶系统自由运动特性，也能分析系统在外界作用下的运动特性，并能确定系统运动的性能指标，如运动时间，运动速度，最大超调量等。

非线性特性可以具有不同的形式。但在用相平面法进行分析时，都有一个共同的思想，即根据非线性特性，将相平面划分为若干区域，每个区域均可用一个二阶线性微分方程来描述，然后求解这个二阶微分方程，绘制相轨迹，平滑地将不同区域的相轨迹连起来，得到整个非线性系统的相轨迹，结合对奇点类型的讨论，就可以用来分析非线性系统的运动特性。

用相平面法分析非线性系统的步骤如下：

①根据非线性特性将相平面划分为若干区域，建立每个区域的线性微分方程来描述系统的运动特性；

②根据分析问题的需要，适当选择相平面坐标轴，通常为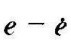，或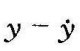作为相平面的坐标轴；

③根据非线性特性建立相平面上切换线方程，必须注意的是，切换线方程的变量应与坐标轴所选坐标变量一致；

④求解每个区域的微分方程，绘制相轨迹；

⑤平滑地将各个区域的相轨迹连起来，得到整个系统的相轨迹。据此可用来分析非线性系统的运动特性。

例8-5 如图8-36所示非线性控制系统在t＝0时加上一个幅度为6的阶跃输入，系统的初始状态为，e（0）＝6，问经过多少秒，系统状态可到达原点。

图8-36 继电控制系统

解 列写运动方程

又

于是有

区域①

代入初始条件有 c1＝0，c2＝6。

图8-37 例8-5题图

相轨迹为一抛物线，如图8-37所示系统从A 出发到达B点，进入区域②。B点坐标可求得

区域②

代入初始条件求得c3＝﹣2，c4＝2。

系统沿抛物线从B点运动到C点，进入区域①，C点坐标可求得为（﹣1，1）。

区域①

由初始条件c（﹣1，1）可求c5＝1，c6＝﹣1。

系统沿抛物线由C点运动到原点。由A 点出发运动到原点O的时间tAO可由下式求得

tAO＝tAB＋tBC＋tBO

由各区域运动方程可分别求得(www.xing528.com)

tAB＝4s，tBC＝6s，tco＝2s

所以

tAO＝4＋6＋2＝12s

例8-6 非线性系统结构如图8-38所示。其中a＝1，tanαa1＝1，。试作系统从初始状态y（0）＝﹣1，出发的相轨迹，概略地画出对应的y（t）曲线。并求出y（t）＝0时的各t值。当y（t）为周期运动时，求出运动周期的值。

图8-38 非线形系统控制

解 列写运动方程

当r＝0时，e＝﹣y。代入上式得到

区域①

所以

代入初始条件A （﹣1，1），求得c1＝﹣1，c2＝﹣1。

系统的相轨迹为一圆弧，如图8-39所示，由A 运动到B（﹣1，1）进入区域②。

区域②

代入初始条件B（﹣1，1），c3＝1，c4＝﹣1。

系统相轨迹为一平行横坐标轴的直线，系统由B 运动到C （0，1）进入区域③。

图8-39 非线形系统相轨迹

区域③

由初始条件C（0，1），可求c5＝0，。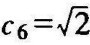

系统相轨迹为一椭圆，系统由C点运动到D（0，﹣1），又一次进入区域②。

区域②

由D（0，﹣1）求得c7＝﹣1，c8＝0。

系统相轨迹为一直线，由D点运动到A点，形成封闭的相轨迹，系统会产生周期运动，由上述各式可求运动周期

由上述各式可概略画出y（t）曲线如图8-40所示。

图8-40 系统输出y（t）概略曲线图