令
x1＝x
则有
写成一般形式有
于是有
只要P（x1，x2），Q（x1，x2）是解析的，则可在给定平衡点附近展开成台劳级数，微分方程（8-42）在给定初始条件下的解是惟一的，于是在以x1为横坐标轴，x2为纵坐标的平面上绘制一条x2与x1的关系曲线，我们把这样一条轨线称为相轨迹，由一族相轨迹组成的图像称为相平面图。而式（8-43）是相轨迹上某点处切线的斜率。
相轨迹反映了非线性微分方程解的关系，具有一些基本特点。首先，由于微分方程解的存在性和惟一性定理可知，相轨迹上除平衡点外的任意一点只有一根相轨迹通过。
令
联立求解出的点（x10，x20）称为系统平衡点。(www.xing528.com)
由式
可知，相轨迹在平衡点附近切线斜率不定，意味着有无穷多根相轨迹到达或离开平衡点。
由于P（x1，x2），Q（x1，x2）是非线性的关系，因此，无法用解析方法绘制相轨迹。只能采用近似作图的方法绘制相轨迹。这里仅介绍等倾线法来绘制相轨迹。
由式（8-43）有
称为相轨迹方程，反映了x2和x1之间关系。而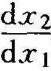
绘出了相轨迹上在点（x1，x2）处的切线的斜率。如果令
α为一常数。
则
上式为x1和x2之间的代数方程，根据上式可在相平面上绘制一条线，在这条线上的各点具有一个共同的性质，相轨迹通过这些点时，其切线的斜率都相同，我们称之为等倾线。如果取不同的值α1，α2，⋯则可在相平面上绘制一系列的等倾线。如图8-27所示。在每一根等倾线上画出相应的α值短线，以表示相轨迹通过这些等倾线时切线的斜率。相平面中所有等倾线上的短线，组成了相轨迹的切线场。如果任意给定一初始条件（x10，x20），就相当于在相平面上给定了一条相轨迹的起点，从该点出发，平滑的将相邻等倾线上的短线连起来，就得到所要求的系统的相轨迹。要得到较为精确的相轨迹，只要尽可能多地给出α值，在相平面上绘制更密的等倾线。
图8-27 用等倾线法绘制相轨迹
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
