正如描述函数的定义指出,一个非线性环节的描述函数只是描述环节在正弦信号作用下,其输出基波分量与输入正弦的关系。显而易见它不能像线性系统的频率特性那样全面反映线性环节的动力学特性。但在实际非线性系统的分析中,我们最关心的是系统是否会产生自激振荡。如果系统一旦产生自激振荡,由于线性部分的低通滤波特性,非线性环节的输入可近似看做正弦输入,于是可用描述函数来描述非线性环节的动态特性,据此可用描述函数来分析整个系统动力学特性,系统是否稳定,系统是否会产生自激振荡。如果一旦产生自激振荡,如何求出自激振荡参数(即自激振荡振幅和振荡频率),进而寻求克服自激振荡的方法。
一非线性系统结构如图8-21所示,假定输入为零,现来分析一下系统产生自激振荡的条件,进而将线性系统中奈奎斯特判据推广应用于非线性系统,判断系统稳定性。
图8-21 非线性系统
图中G1,H,G2为线性部分的传递函数,N(A)为非线性环节的描述函数,假定X2=A2sinωt,则
式中
假定
则非线性环节的输出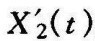 为
为
如果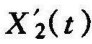 等于X2(t),则意味着产生了自激振荡,从而可推出系统产生自激振荡的条件为
等于X2(t),则意味着产生了自激振荡,从而可推出系统产生自激振荡的条件为
∣N(A)G1(jω)G2(jω)H(jω)∣=1(8-35)
θ+Φ=(2n+1)π(8-36)
令线性部分的传递函数为G(s)
G(s)=G1(s)G2(s)H(s)
综合式(8-35)、式(8-36)可得出系统产生自激振荡的条件为
系统一旦产生自激振荡,意味着在同一比例尺下的复平面上,G(jω)轨线与负倒描述函数曲线有交点。由幅值条件和相角条件,得到两个方程式,可联立求解出自激振荡的振幅和振荡频率。
由式(8-37),将奈奎斯特判据推广应用于非线性系统,可判断系统运动稳定性:线性部分为最小相位系统,若G(jω)轨线不包围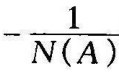 轨线,则系统是稳定的,若G(jω)轨线包围
轨线,则系统是稳定的,若G(jω)轨线包围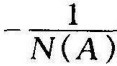 轨线,则系统是不稳定的若G(jω)与
轨线,则系统是不稳定的若G(jω)与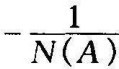 相交,则意味着系统会产生自激振荡,交点处G(jω)曲线所对应的角频率ω为自激振荡的角频率,交点处-
相交,则意味着系统会产生自激振荡,交点处G(jω)曲线所对应的角频率ω为自激振荡的角频率,交点处-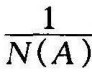 所对应的幅值A为自激振荡的振幅值。)
所对应的幅值A为自激振荡的振幅值。)
图8-22所示G(jω)与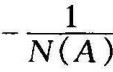 的相互关系曲线。
的相互关系曲线。
图8-22 G(jω)曲线与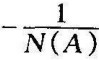 曲线相互关系
曲线相互关系
应用推广的奈氏判据可知图8-22(a)所对应的非线性系统是稳定的,图8-22(b)和(c)所对应的非线性系统是不稳定的,因为G(jω)曲线包围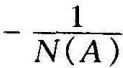 轨线。而图822(d)所对应的系统会产生自激振荡,因为G(jω)与
轨线。而图822(d)所对应的系统会产生自激振荡,因为G(jω)与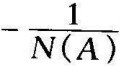 相交与a点和b点,会产生自激振荡。
相交与a点和b点,会产生自激振荡。
下面分析一下a点和b点对应的自激振荡,其中必有一个是稳定的自激振荡状态,另一个是不稳定的自激振荡状态,现实的物理系统只会产生一个稳定的自激振荡。
假定给a 点对应的自激振荡状态一个扰动,使得振幅增加,由a 点跑到a″点,由于a″点被G(jω)曲线包围,系统是不稳定的,a″点对应的振幅会进一步增加,再也回不到a点。假定给a点的扰动使之跑到a点,即振幅减小,由于a点不被G(jω)曲线包围,系统是稳定的,系统产生衰减振荡,即振荡振幅进一步减小,系统再没能力使a′点回到a点,因此,a点对应的自激振荡状态是不稳定的自激振荡状态。用类似分析方法,可以知道b点所对应的自激振荡状态是稳定的自激振荡状态。
自激振荡的振幅和振荡频率由下面二式求得
∣G(jω)N(A)∣=1(8-38)
θ+Φ=﹣π(8-39)
例8-2 一继电控制系统结构如图8-23所示。继电器参数a=1,b=3,试分析系统是否产生自激振荡,若产生自激振荡,求出振幅和振荡频率。若要使系统不产生自激振荡,应如何调整继电器参数。
图8-23 继电控制系统
解 带死区的继电特性的描述函数为
当A→a时,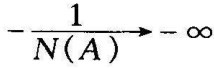 ;
;
A→∞时,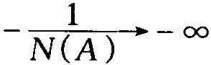 。
。
可见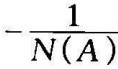 在负实轴上有极值点。
在负实轴上有极值点。
令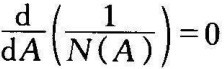 ,求得极值点(https://www.xing528.com)
,求得极值点(https://www.xing528.com)
将a=1,b=3代入下式
图8-24 G(jω)与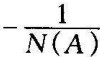 曲线
曲线
又
令虚部为零求得 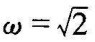
将 代入实部求得
代入实部求得
由此可见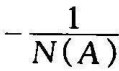 与G(jω)有交点,如图8-24所示。为求得交点处对应的振幅值,令
与G(jω)有交点,如图8-24所示。为求得交点处对应的振幅值,令
求得两个振幅值 A1=1.11,A2=2.3
经过分析系统会产生一个稳定的自激振荡,自激振荡的振幅为2.3,振荡频率为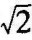 。
。
为使系统不产生自激振荡,可令
可求得继电器参数比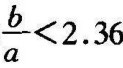 。
。
按上式调整a 和b比例为b=2a,即可保证使系统不产生自激振荡。
例8-3 已知一多环控制系统如图8-25所示。当G1(s)=1时,该系统工作在饱和特性线性段时的无阻尼自然振荡频率ωn=2,阻尼比ζ=1。当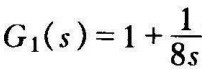 时,求使系统稳n定的最小比值
时,求使系统稳n定的最小比值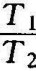 。
。
图8-25 多环控制系统
解 当G1(s)=1时,多环系统的闭环传递函数为
所以
令
所以
当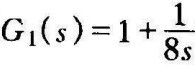 时,由闭环系统的特征方程
时,由闭环系统的特征方程
可知
由于T1和T2参数未知,G(jω)曲线有三种可能性,如图8-26中虚线①、②、③,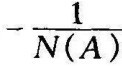 曲线也画在图中。为确保系统能稳定运行,所选择的参数T1和T2应能使G(jω)曲线具有曲线③的形状。曲线③和曲线②、曲线①的最大区别在于它与负实轴没有交点。为此令G(jω)的虚部等于零
曲线也画在图中。为确保系统能稳定运行,所选择的参数T1和T2应能使G(jω)曲线具有曲线③的形状。曲线③和曲线②、曲线①的最大区别在于它与负实轴没有交点。为此令G(jω)的虚部等于零
图8-26 G(jω)和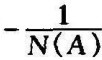 曲线
曲线
求得
只要
则所求ω值为虚数,即能确保G(jω)曲线与负实轴没有交点。
而
T1+T2=1
所以
于是,求得使系统稳定时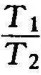 的最小比值为
的最小比值为
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




