探析非线性系统的特点

非线性系统与线性控制系统相比，具有一系列新的特点。

①线性系统满足叠加原理，而非线性控制系统不满足叠加原理。

所谓叠加原理要满足叠加性和均匀性两方面的要求。即当给定系统输入为X1，其输出为Y1，当给定系统输入为X2，其输出为Y2，当给定系统输入为X1＋X2，其输出为Y1＋Y2，对线性系统而言，则称系统满足了叠加性；但对非线性系统而言，利用非线性滤波，也可使系统满足叠加性。如图8-1所示非线性系统。非线性器件Ⅰ，当输入为X1时，其输出为Y1，非线性器件Ⅱ的输入为X2时，其输出为Y2，而滤波器Ⅰ对X1具有良好的滤波特性，它只允许X1通过；而滤波器Ⅱ，设计它的滤波特性，只允许X2通过，这样的非线性装置也可满足叠加性，即当输入为X1＋X2时，其输出为Y1＋Y2。

图8-1 带滤波器的非线性系统

虽然如此，判断一个装置是线性的还是非线性的第二个要求是所谓均匀性。即当装置输入为X1时，其输出为Y1，当输入为nX1时，其输出为nY1。此时，只有线性装置满足这个要求，而非线性装置无论如何不可能满足均匀性。

②线性定常控制系统的稳定性仅取决于控制系统的固有结构和参数，而与系统的初始条件以及外加输入没有关系。

而对非线性系统而言，甚至没有笼统的有关整个非线性系统的稳定性概念。对非线性控制系统，总是针对某一平衡点而言，讨论其运动稳定性问题。如果在某一初始扰动范围内，系统有能力使系统维持在某一平衡状态，就称该运动状态在一定范围内是稳定的。如果，系统没有能力维持该平衡点的运动状态，就称该平衡点的运动状态是不稳定的。非线性系统平衡点的运动状态是极其复杂的。平衡点的运动稳定性不仅与系统的固有结构和参数有关，还与系统的输入大小，扰动的大小以及系统的初始状态有关。下面，通过一简单实例来说明这个问题。

对于一由非线性微分方程

描述的非线性系统，显然有两个平衡点，即x1＝0和x2＝1。下面讨论一下这两个平衡点的运动稳定性问题。将上式改写为

设t＝0时，系统的初态为x0。积分上式可得

当初始条件x0＜1时，随着时间趋于∞时，x（t）趋于零。这意味着，x＝0的平衡状态在受到干扰后，只要使x＜1时，系统有能力恢复到渐近零平衡状态，这说明，x＝0的平衡状态是小范围稳定的。当x0＞1时 当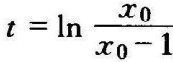时，x（t）趋于∞，这说明x＝1的平衡状态，在受到干扰后，要么趋于∞，要么趋于零，说明x＝1的平衡状态是不稳定的。如图8-2所示。(www.xing528.com)

图8-2 一阶非线性系统

由上面分析可知，不能笼统地说非线性系统是否稳定，我们总是针对系统平衡状态的运动稳定性来加以讨论的。这是非线性系统不同于线性系统的地方。

③线性系统在没有外作用时，系统的周期运动只能发生在无阻尼状态，即系统特征方程的根为一对共轭纯虚根。而且，这种等幅运动状态，对于实际的物理系统是不存在的。因为一旦系统中的某一物理参数随外界环境发生变化时，系统特征方程的根要么处于左半S平面，要么处于右半S平面。对于前者，系统是稳定的，系统产生衰减振荡。对于后者，系统不稳定，系统将产生发散振荡。无论如何，线性系统不可能维持稳定的等幅运动状态。

对于非线性系统而言，在没有外加周期信号作用时，其系统自由运动完全可能发生稳定的等幅运动状态。例如，各种信号发生器正是利用非线性装置的最好实例。把这种等幅运动状态称为自激振荡，对于二阶非线性系统，称这种自激振荡状态为极限环。

④线性系统在正弦信号作用下，系统输出的稳态分量为同频率的正弦信号，只不过输出振幅和初始相位发生变化，这正是频率法分析线性系统的基础。

而非线性系统在正弦信号作用下，其输出存在极其复杂的情况。

a.跳跃谐振和多值响应这是在某些非线性系统中特有的现象。如图8-3所示的非线性弹簧输出的幅频特性。当维持外加输入信号幅值不变时，而其角频率ω逐渐增加时，系统输出幅值A（ω）沿着曲线1-2-3变化，若ω继续增加时，非线性系统产生由3到4的跳跃，输出幅值A（ω）产生跳跃变化，若ω继续增加，系统输出幅值A（ω）沿4-5变化。当角频率由大向小的方向减小时，系统幅值A（ω）沿5-4-4′变化，在ω发生跳跃谐振由4′→2′变化，当ω继续减小时，系统输出幅值A（ω）沿2′→1变化。把在ω′和ω″点发生的跳跃变化，称为跳跃谐振。在对应ω′～ω″段系统输出幅值A（ω）对应两个幅值，这种现象称为多值响应。

图8-3 跳跃谐振与多值响应

b.分频振荡和倍频振荡 非线性系统在正弦信号作用下，其稳态分量除产生同频率振荡外，还可能产生倍频振荡和分频振荡。即输出振荡频率是输入信号频率整数倍的倍频振荡和周期是输入信号整数倍的分频振荡。如图8-4所示波形。