离散控制系统的瞬态响应优化

离散系统的动态特性，是通过在外加输入信号作用下，其输出曲线来反映的。通常给定输入为单位阶跃。瞬态响应分析焦点放在闭环零极点对瞬态响应的定性影响，而不是从定量上来分析，定量分析比起连续系统来说更为复杂。另外，还将介绍一种离散瞬态响应，即闭环极点都分布在原点时所产生的瞬态响应，具有新的特点，其过渡过程能在有限时间内结束，这是与连续系统不同的瞬态响应，并由此带来快速数字随动系统的新课题。

（1）闭环零极点与瞬态响应的关系

通常离散控制系统的闭环脉冲传递函数可表示为如下形式

当系统输入为单位阶跃时，其系统输出Y（z）为

展开成部分分式，有

式中

式（7-95）中第一项为闭环系统输出的稳态分量，第二项为闭环系统输出的瞬态分量。下面分析一下闭环极点对系统瞬态响应的影响。

①Pk为正实根，对应的瞬态分量

令Pk＝eaT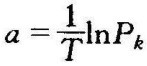，则

若Pk＝1，即闭环极点位于右半Z平面上圆周上，闭环系统瞬态响应yk（nT）为等幅脉冲，对应图7-39中a点对应波形。

若Pk＜1，则闭环极点位于单位圆内，此时a＜0，则输出响应yk（nT）呈指数衰减状，如图7-39中b点对应波形。

若Pk＞1，闭环极点位于单位圆外，此时a＞0，则输出响应yk（nT）呈指数增加状，如图7-39中c点对应波形。

②当Pk为负实根，则对应的瞬态分量为

若Pk＝﹣1，输出响应分量yk（nT）对应图7-39中d点波形，呈等幅跳跃输出。

图7-39 闭环实极点分布与相应瞬态响应

若∣Pk∣＜1，输出响应分量yk（nT）对应图7-39中e点波形。

若∣Pk∣＞1，输出响应分量yk（nT）对应图7-39中d点波形，呈发散跳跃变化。

③当Pk，Pk＋1为一对共轭复根时，为

此时，Ck，Ck＋1也为一对共轭复数。

则它们对应的瞬态分量yk，k＋1（nT）为(www.xing528.com)

若∣Pk∣＜1，则对应的瞬态响应分量为振幅衰减的正弦振荡，对应图7-40中a点对应的波形。

图7-40闭环共轭复极点与相应的瞬态响应

若∣Pk∣＞1，则对应的瞬态响应分量为发散正弦振荡，对应图7-40中b点对应的波形。

令式（7-101）中θk为

θk＝ωT（7-102）

所以

为系统对应瞬态分量的振荡频率，其振荡周期

由上式可求在一个振荡周期Td中，所包含的脉冲个数，这有利于实际离散系统的调试。设一个振荡周期中所包含的脉冲个数为n，采样周期为T，则

所以

例7-29 一采样控制系统，其闭环脉冲传递函数的极点分布如图7-41所示，若采样周期为T，试计算该系统阶跃响应的衰减振荡周期Td，及每个衰减振荡周期中所包含的脉冲个数n。

解 衰减振荡周期

图7-41 闭环脉冲传递函数的极点分布

即每个衰减振荡周期包含4个采样脉冲。

（2）有限时间响应系统

当闭环脉冲传递函数所有极点都分布在原点时，此时的系统具有一个很特别的响应，即在有限时间内结束过渡过程，达到稳态，此时的闭环脉冲传递函数具有如下形式

其单位脉冲响应

即在单位脉冲作用下，该系统的瞬态响应能在nT内结束，即n拍可结束过渡过程，这个特点是连续系统所不具备的。但是，值得注意的是：由于调整时间太短，作用于对象的控制需要很强。系统会受饱和特性的影响，从而将改变系统的实际性能；所有极点均在Z平面上的原点，这个条件太苛刻了。实际上，系统参数不会是恒定不变的。参数的稍微变化会使系统的性能变得很差；这种系统对输入信号的适应性很差。

这种系统的综合将在后面予以详细论及。