线性离散控制系统稳定性分析

线性连续控制系统稳定性概念、稳定性条件、稳定性判据，前面已经作了详细讨论。把对线性微分方程解的稳定性问题，通过拉氏变换，转化为分析系统特征方程的根是否具有负实部的问题，又根据代数方程根与系数的关系，提出劳斯代数稳定性判据，并在S平面上建立起稳定域，即特征方程的根处于左半S平面，则系统是稳定的结论。

线性离散控制系统的闭环脉冲传递函数，如图7-30所示，可求得为

则线性离散控制系统的特征方程为

图7-30 线性离散控制系统

1＋G（z）＝0（7-84）

由于在S平面，离散控制系统的特征方程是含s的超越函数，分析十分困难，求解有关s的特征方程的根几乎不可能，通过Z变换将S域的问题转化为Z域的分析问题。首先要建立起这种影射关系，从而得出在Z域内，线性离散系统稳定的充分必要条件。

考察下式

z＝e Ts（7-85）

假定在S平面上任有一点

s＝δ＋jω（7-86）

则通过Z变换，映射到Z平面为

z＝eδT·ejωT（7-87）

当δ＝0，即S平面的虚轴，对应Z平面的单位圆。

当δ＜0，即左半S平面对应Z平面的单位圆内部区域，即S平面的稳定域映射到Z平面单位圆内的区域为稳定区域。

当δ＞0，即右半S平面对应Z平面的单位圆外部区域，也即S平面不稳定域映射到Z平面单位圆外的部分为不稳定域。上面映射关系如图7-31所示。

图7-31 S平面到Z平面映射

通过上面分析，得出线性离散控制系统稳定的充分必要条件是：线性离散闭环控制系统特征方程（7-84）的根的模小于1，则线性离散控制系统是稳定的。

例7-25 已知离散控制系统结构如图7-32所示，采样周期T＝1s，分析系统的稳定性。

解

闭环特征方程

1＋G（z）＝0

z2＋4.952z＋0.368＝0

图7-32 离散控制系统

z1＝﹣0.076，z2＝﹣4.876

系统特征方程的根有一个在单位圆外，因此，该离散系统不稳定。

对于特征方程的阶次大于2以上的系统，用直接求特征方程根的办法来判断系统是否稳定，显然是不可能的。在离散系统中，由于是在Z平面分析，不能直接应用劳斯代数判据，为了能应用劳斯代数判据，引进双线性映射。

令

或

其中z和ω均为复变量，可写为

z＝x＋jy（7-90）

ω＝u＋jυ（7-91）

将式（7-90）代入式（7-89），有

于是，当x2＋y2＝1 即对应Z平面上的单位圆

u＝0 即w平面上的虚轴

当x2＋y2＜1 即Z平面上单位圆内的部分，也即稳定域

u＜0 即左半w平面为稳定域

当x2＋y2＞1 即Z平面上单位圆内外的部分，也即不稳定域

u＞0 即右半w平面对应不稳定域

上面映射关系如图7-33所示。

图7-33Z平面到W平面的映射

经过Z平面到w平面的映射后，就可在w平面上应用劳斯代数判据了。因为，此时左半w平面为系统稳定域，而右半w平面为不稳定域。

例7-26 已知离散控制系统如图7-34所示，采样周期T＝0.2s，分析离散控制系统的稳定性。

图7-34 离散控制系统的稳定性

解开环系统脉冲传递函数G（z）(www.xing528.com)

闭环特征方程

1＋G（z）＝0

得到

z3－1.001z2＋0.3356z＋0.00535＝0

作w变换，令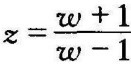，代入上式，经整理得

2.33ω3＋3.68ω2＋1.65ω＋0.34＝0

列出劳斯表

ω3 2.33 1.65

ω2 3.68 0.34

ω1 1.43 0

ω0 0.34

劳斯表中第一列全为正，该离散系统是稳定的。

由于分析离散系统稳定性是建立在Z变换的基础上，而Z变换仅反映离散系统在采样时刻系统的信息，并不反映在两个采样时刻间系统的信息，因此在用Z变换分析系统时会带来局限性。

首先，在稳定性分析中，用Z变换表达式分析离散系统是稳定的，而实际物理系统的输出是连续波形，因此，可能存在潜伏振荡问题，如图7-35所示。

图7-35 离散系统的潜伏振荡

图7-35（a）描述的是在单位阶跃下，离散输出是稳定的，但实际物理系统输出产生等幅震荡。图7-35（b）显示的离散系统在单位阶跃下，其离散输出是按非周期包络线达到稳态的，而实际物理系统的输出可能是衰减振荡的。这就是所谓潜伏振荡问题。有时，用离散系统理论来分析离散系统是稳定的，而实际物理系统却是不稳定的或有振荡产生，因此，在调试实际的离散系统时要注意到这一现象可能是合理的，这也正是Z变换理论在系统分析中的局限性。

一般情况下，连续系统加采样开关变为离散系统后，其稳定性可能变坏。当然也有某些特殊情况，例如大滞后的连续系统加采样开关变为离散系统后，也可能改善稳定性。

例7-27 已知离散系统结构如图7-36所示。该系统没有采样开关时，它就是一个二阶连续系统。它是一个绝对稳定的系统，只要K大于零。但加了采样开关后（T＝0.1），变为离散系统，现用Z变换理论来求出使离散系统稳定的K的取值范围。

图7-36离散系统稳定的K的取值范围

解 开环脉冲传递函数为

闭环离散系统的特征方程

1＋G（z）＝0

得到

z2＋（0.632K－1.368）z＋0.368＝0

令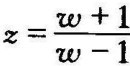，代入上式，经整理得到

0.632Kω2＋1.264ω＋2.736－0.632K ＝0

利用劳斯代数判据，可求得使系统稳定的K的取值范围为

0＜K＜4.32

最后要说明的一点是，离散控制系统的稳定性除与系统固有结构和参数有关外，还与系统的采样周期有关，这是与连续控制系统分析相区别的重要一点。

例7-28 已知离散控制系统结构如图7-37所示，分析离散系统稳定性与采样周期的关系。

图7-37 离散系统稳定性与采样周期的关系

解开环脉冲传递函数G（z）

令e﹣T＝a，则闭环特征方程1＋G（z）＝0经整理为

z2＋（T－2）z＋1－Ta＝0

令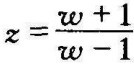，代入上式，经整理得到

（T－Ta）ω2＋2aTω＋4－T－Ta＝0

从而求得使系统稳定的T的取值范围

由于T总是取大于零的数，因此，可以认为要是采样系统稳定采样周期不能大于等于4s。

当T＝1s时，离散系统单位阶跃响应可求得如下

其输出响应见图7-38（a）。

图7-38输出响应与采样周期关系

当T＝4s时，离散控制系统的单位阶跃响应求得如下

其输出响应如图7-38（b）。