Z反变换的三种方法及其应用

拉氏变换引进动力系统分析，可将求解微分方程问题变为求解代数方程，由传递函数可求系统的时域响应，只需求拉氏反变换而已。这就大大简化了对系统的分析。

Z变换有同样的优点，它将分析差分方程问题变为分析代数方程问题，通过求X（z）的原函数x（kT）或x*（t），可求出离散系统的时域响应。

这里介绍三种Z反变换的方法。

（1）幂级数法

通常Z变换表达式有如下形式

实际的物理系统满足n≥m，则用综合除法有

由Z变换的定义式可知

x（kT）＝ck

则

即为X（z）的原函数。

例求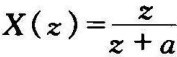的原函数X（k）。

解

所以

x（k）＝（－a）k

（2）部分分式法

部分分式法又称查表法。它的基本思想是将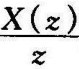展开成部分分式

然后，查Z变换表（附表），即可求取X（z）的原函数x（kT）。

例7-14 已知

求x（kT）。(www.xing528.com)

解

所以

查Z变换表有

x（kT）＝1－e－akT

所以

（3）留数法

由Z变换的定义式有

上式两端乘以zk－1有

X（z）zk－1＝x（0）zk－1＋x（T）zk－2＋⋯＋x（kT）z﹣1＋⋯ （7-44）

上式为罗朗级数，x（kT）是z﹣1项的系数，根据复变函数中求罗朗级数系数的公式，得

在此，积分路径包围X（z）zk－1的所有极点。根据留数定理，则上式可写成

x（kT）＝∑Res[X（z）zk-1] （7-46）

式中Res[·] 表示函数的留数。上式表明，x（kT）等于X（z）zk－1在其所有极点上的留数之和。

例7-1 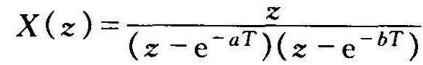，求x（kT）。

解

例7-16，求x（kT）。

解