【摘要】：由式（7-5）可知，断续函数x*的拉氏变换为若令eTs＝z 则将在S域分析的问题变成Z域的分析问题。例7-4 已知函数，求它们的Z变换表达式。这正好说明了Z变换方法的局限性，它仅考查时域函数在采样时刻的特性。由于单位阶跃函数和单位脉冲序列函数在采样时刻具有相同特性，因此，其Z变换表达式具有相同形式。解 因为所以上面几个简单实例都是基于Z变换的定义来求解的，对于较复杂的函数求Z变换表达式时，可以用如下公式法。
由式（7-5）可知，断续函数x*（t）的拉氏变换为
若令
eTs＝z （7-29）
则将在S域分析的问题变成Z域的分析问题。
X（z）称为x*（t）的Z变换，记为Z[x*（t）]
在Z变换中，X（z）为采样脉冲序列的Z变换，即只考虑采样时刻的信号值。由于在采样时刻，x（t）的值就是x（kT），所以从这个意义上说，X（z）既是x*（t）的Z变换，也可以写为x（t）的Z变换，即
下面举几个例子说明Z变换的求法，并通过实例说明Z变换方法的局限性。
例7-4 已知函数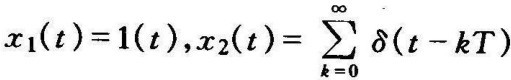
，求它们的Z变换表达式。
解
从上例可以看出单位阶跃函数和单位脉冲序列函数在时域特性上是两个不同的函数，但它们具有相同的Z变换表达式。这正好说明了Z变换方法的局限性，它仅考查时域函数在采样时刻的特性。由于单位阶跃函数和单位脉冲序列函数在采样时刻具有相同特性，因此，其Z变换表达式具有相同形式。今后，碰到更为复杂情况时，是值得注意的问题。
例7-5 已知x（t）＝e﹣at，求X（z）。
解
例7-6 已知x（t）＝t，求X（z）。
解(www.xing528.com)
例7-7 已知x（t）＝sinωt，求X（z）。
解 因为
所以
例7-8 已知 ，求G（z）。
解 因为
所以
上面几个简单实例都是基于Z变换的定义来求解的，对于较复杂的函数求Z变换表达式时，可以用如下公式法。
已知G（s），若si为G（s）的极点，则
式中
例7-9 已知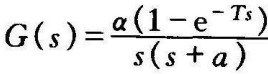
，求G（z）。
解
所以
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
