如何选择采样周期？

采样定理只是给出了采样周期选择的基本原则，即从信号恢复的角度出发，给出采样周期T的下限，不得小于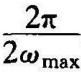。至于到底选择采样周期T等于多少，涉及许多因素。在下面各节离散系统分析中可以看出，采样周期T将影响采样系统的稳定性，稳态误差及动态响应，我们必须综合各种因素，根据特定的控制目标，来确定采样周期。

在一般工业过程控制中，微型计算机所能提供的运算速度，对于采样周期的选择来说，回旋余地较大。工程实践表明，根据表7-1给出的参考数据选择采样周期T，可以取得满意的控制效果。但是，对于快速随动系统，采样周期T的选择将是系统设计中必须予以认真考虑的问题。采样周期的选择，在很大程度上取决于系统的性能指标。

表7-1 工业过程T的选择

从频域性能指标来说，控制系统的闭环频率响应通常具有低通滤波特性，当随动系统的输入信号的频率高于其闭环幅频特性的谐振频率ωr时，信号通过系统将会很快衰减，因此可认为通过系统的控制信号的最高频率分量为ωr。在随动系统中，一般认为开环系统的截止频率ωc与闭环系统的谐振频率ωr相当接近，近似有ωc＝ωr，故在控制信号的频率分量中，超过ωc的分量通过系统后将被大幅度衰减掉。工程实践表明，随动系统的采样角频率可近似取为

ωs＝10ωc（7-13）(www.xing528.com)

由于T＝2π/ωs，所以采样周期可按下式选取

从时域性能指标来看，采样周期T可通过单位阶跃响应的上升时间tr或调整时间ts按下列经验公式选取

或者

应当指出，采样周期选择得当，是连续信号e（t）可以从采样信号e*（t）中完全复现的前提。然而，图7-8所示的理想滤波器实际上并不存在，因此只能用特性接近理想滤波器的低通滤波器来代替，零阶保持器是常用的低通滤波器之一。为此，需要研究信号保持过程。