Matlab为系统校正提供了方便的工具，改变校正装置的参数，可清楚地看到校正对系统性能的影响。下面例题给出了Matlab语句的应用，读者还可根据问题的需要，自己编写合适的函数，使程序更加简洁。
例6-9 单位反馈系统的开环传递函数为
试确定串联校正装置的特性，使系统满足在斜坡函数作用下系统的稳态误差小于0.1，相角裕度γ≥45°。
解根据系统稳态精度的要求，选择开环增益K＝12，求原系统的相角裕度。
＞＞num＝12；
den＝[2，1，0]；
[gm，pm，wcg，wcp] ＝margin （num，den）；
[gm，pm，wcg，wcp]
margin （num，den）
ans＝
Inf 11.6548 Inf 2.4240
可知，原系统相角裕度为γ＝11.6°，ωc＝2.4rad/s，不满足指标要求，系统的Bode如图6-34所示。考虑采用串联超前校正装置，以增加系统的相角裕度。
图6-34 原系统的Bode图
选择超前校正装置的最大超前相角φm＝40°，则有
为使超前装置的相角补偿作用最大，选择校正后系统的剪切频率在最大超前相角发生的频率上，由图6-34，当幅值为﹣10lga＝﹣10lg4.77＝﹣6.8dB时，相应的频率为3.6rad/s。选择此频率作为校正后系统的剪切频率
由式（6-12）确定参数T
初选校正装置的传递函数为
校正后系统的开环传递函数为
校正后系统的Bode图如图6-35所示。(www.xing528.com)
由图可知，校正后系统的相角裕度为47°，满足性能指标的要求，故该超前装置即为所求。
图6-35 校正后系统的Bode图
例6-10 设控制系统的开环传递函数为
试设计一申联校正装置，使校正后系统的相角裕度不小于40°，幅值裕度不低于10dB，剪切频率大于（1rad/s）。
解 作校正前系统的对数频率特性。
＞＞num＝8；
den＝[0.125，0.75，1，0]；
margin（num，den）
[gm，pm，wcg，wcp]
ans＝
0.7500 ﹣7.5156 2.8284 3.2518
程序运行后，得到图6-36。
由图6-36可知，原系统具相角裕度和幅值裕度均为负值，故系统不稳定。考虑到系统的剪切频率为3.3rad/s，大于系统性能指标要求的剪切频率，故采用滞后装置对系统进行校正。
根据相角裕度γ≥40°的要求和滞后装置对系统相角的影响，选择校正后系统的相角裕度为γ′＝40°＋6°＝180°＋（﹣134°），由图6-36知，对应相角为﹣134°时的频率为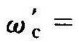
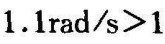，幅值为15.7dB。
取201gb＝﹣15.7dB，得b＝0.164。取滞后装置的第二个转折频率为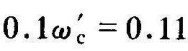
，有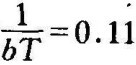
，则T＝55.43。初选校正装置的传递函数为
作出校正后系统的Bode图如图6-37中所示。由图可得到校正后系统的相角裕度为γ＝40.67°，幅值裕度为12.73dB，剪切频率为ωc＝1.1rad/s，满足系统性能指标的要求，故初选校正装置合适，校正后系统的开环传递函数为
图6-36 校正前系统的对数幅频特性
图6-37 校正后系统的Bode图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
