控制系统反馈校正的方法与意义

在控制系统的校正中，反馈校正也是常用的校正方式之一。反馈校正除了与串联校正一样，可改善系统的性能以外，还可抑制反馈环内不利因素对系统的影响。

图6-31 具有反馈校正的系统

图6-31表示一个具有局部反馈校正的系统。在此，反馈校正装置H（s）反并接在G2（s） G3（s）的两端，形成局部反馈回环（又称为内回环）。为了保证局部回环的稳定性，被包围的环节不宜过多，一般为2个。

由图知，无反馈校正时系统的开环传递函数为

G（s）＝G1（s）G2（s）G3（s）G4（s）（6-35）

内回环的开环传递函数为

G′（s）＝G2（s）G3（s）H（s）（6-36）

其闭环传递函数为

校正后系统的开环传递函数为

若内回环稳定（即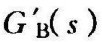的极点都在左半S平面），则校正后系统的性能可按20lg∣G″（jω）∣曲线来分析。绘制20lg∣G″（jω）∣，假定以下两点。

①当∣G′（jω）∣1时，1＋G′（jω）≈G′（jω），于是按式（6-38）

由20lg∣G（jω）∣与20lg∣G′（jω）∣之差，便得20lg∣G″（jω）∣。

②当∣G′（jω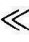）∣1时，1＋G′（jω）1，则

G″（jω）≈G（jω）（6-40）

201g∣G″（jω）∣曲线与201g∣G（jω）∣曲线重合。这样近似处理，显然在∣G′（jω）∣＝1附近的误差较大。校正后系统的瞬态性能主要取决于20lg∣G″（jω）∣曲线在其穿越频率附近的形状。一般，在20lg∣G″（jω）∣曲线的穿越频率附近，∣G′（jω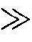）∣1；因此，近似处理的结果还是足够准确的。(www.xing528.com)

综合校正装置时，应先绘制20lg∣G（jω）∣的渐近线，再按要求的性能指标绘制20lg∣G″（jω）∣的渐近线，由此确定20lg∣G′（jω）∣，校验内回环的稳定性，最后按式（6-36）求得20lg∣H（jω）∣。

例6-8控制系统的结构图如图6-32所示，其中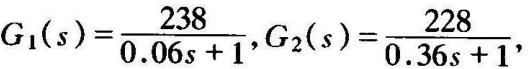，试设计反馈校正装置，使系统的性能指标为：σ≤25％，ts≤0.8s。

图6-32 控制系统结构图

解 校正前系统的开环传递函数为

①绘制原系统的对数幅频特性L0如图6-33所示。

②绘制系统的期望对数幅频特性。

根据式（5-105）和式（5-8），得对应σ≤25％时，Mr≤1.23，按ts≤0.8s，由式（5-106），得ωc≥9.7。取ωc＝10，期望特性的交接频率ω2可由式（6-33）求得。

取ω2＝1.1。

为简化校正装置，取中高频段的转折频率ω3＝1/0.06＝16.7。过ωc＝10作﹣20dB/dec的直线过0dB线，低端至ω2＝1.1处的A点，高端至ω3＝16.7处的B点。再由A点作﹣40dB/dec的直线向低频段延伸与L0相交于C点，该点的频率为ωc＝0.009，过B点作﹣40dB/dec的直线向高频段延伸与L0相交于D点，该点的频率为ωD＝190。由以上步骤得到的期望对数幅频特性如图6-33中LK所示。

图6-33 控制系统的对数幅频特性

③将L0－LK得到20lg∣G2（jω）H（jω）∣，如图中LH所示，其传递函数为

其中

得