期望频率特性校正方法优化

期望频率特性法对系统进行校正是将性能指标要求转化为期望的对数幅频特性，再与原系统的频率特性进行比较，从而得出校正装置的形式和参数。该方法简单、直观，可适合任何形式的校正装置。但由于只有最小相位系统的对数幅频特性和对数相频特性之间有确定的关系，故期望频率特性法仅适合于最小相位系统的校正。

图6-27 期望特性

设希望的开环传频率特性为G（jω），原系统的开环频率特性为G0（jω），串联校正装置的频率特性为Gc（jω），则有

G（jω）＝G0（jω）Gc（jω）

即

其对数频率特性为

Lc（ω）＝L（ω）－Lo（ω） （6-19）

式（6-19）表明，对于已知的待校正系统，当确定了期望对数幅频特性之后，就可以得到校正装置的对数幅频特性。

通常，为使控制系统具有较好的性能，期望的频率特性如图6-27所示。由图可以看出，系统在中频区的渐近对数幅频特性曲线的斜率为﹣40dB～﹣20dB～﹣40dB（即2-1-2型），其频率特性具有如下形式

故相角裕度为

由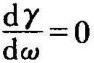可得到产生最大相角裕度γmax的角频率为

式（6-21）说明ωm正好是两个转折频率的几何中心。

由式（6-20）和式（6-21）可得到

所以

图6-28 由等M 圆确定∣G（jωm）

若令对数幅频特性中斜率为﹣20dB/dec的中频段宽度为H，则有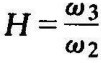，式（6-22）可写成

因为

所以

或

由图6-27和图6-28可得到剪切频率ωc与ωm，ω2，ω3之间的关系，由图6-27，有

若取M r＝M 1＞1，如图6-28所示，可得出

则有

由式（6-27）和式（6-21），有

将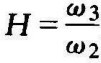及式（6-25）代入式（6-28）得

为使系统具有以H表征的阻尼程度，通常取

若采用Mr最小法，即把闭环系统的频域指标Mr放在开环系统的截止频率ωc处，使期望对数频率特性对应的闭环系统具有最小Mr值，则交接频率ω2和ω3的选择范围是

期望对数幅频特性的求法：

①根据对系统稳态误差的要求确定开环增益K及对数幅频特性初始段的斜率；

②根据系统性能指标，由剪切频率ωc，γ，H，ω2，ω3等参数，绘制期望特性的中频段，并使中频段的斜率为﹣20dB/dec，以保证系统有足够的相角裕度；

③若中频段的幅值曲线不能与低频段相连，可增加一连接中低频段的直线，直线的斜率可为﹣40dB/dec或﹣60dB/dec，为简化校正装置，应使直线的斜率接近相邻线段的斜率；

④根据对幅值裕度及高频段抗干扰的要求，确定期望特性的高频段，为使校正装置简单，通常高频段的斜率与原系统保持一致或与高频段幅值曲线完全重合。

下面通过例题说明用期望对数幅频特性校正系统的步骤和方法。

例6-6 设单位反馈系统的开环传递函数为

试用串联综合校正方法设计串联校正装置，使系统满足：Kv≥70s﹣1，ts≤1s，σ％≤40％。

图6-29 例6-6题对数幅频特性(www.xing528.com)

解 ①根据稳态指标的要求，取K＝70，并画出未校正系统对数幅频特性，如图6-29所示，求得未校正系统的剪切频率

②绘制期望特性，主要参数如下。

低频段 系统为1型，故当ω＝1时，有

20lg∣G0Gc∣＝20lgK＝36.9dB

作斜率为﹣20dB/dec的直线与20lg∣G0∣的低频段重合。

中频及衔接段由式（5-105）及式（5-106），将σ％及ts转换成相应的频域指标，并取为

Mr＝1.6，ωc＝13rad/s

由式（6-33）及式（6-34）估算，有

ω2≤4.88，ω3≥21.13

在ωc＝13处，作﹣20dB/dec斜率的直线，交201g∣G0∣于ω＝45处，见图6-29。取

ω2＝4，ω3＝45

此时，H＝ω3/ω2＝11.25。由式（6-23），有

在中频段与过ω2＝4的横轴垂线的交点上，作﹣40dB/dec斜率直线，交期望特性低频段于ω1＝0.75rad/s处。

高频及衔接段在ω3＝45的横轴垂线和中频段的交点上，作斜率为﹣40dB/dec直线，交未校正系统的20lg∣G0∣于ω4＝50处；ω≥ω4时，取期望特性高频段20lg∣G0Gc∣与未校正系统高频特性20lg∣G0∣一致。

于是，期望特性的参数为

ω1＝0.75，ω2＝4，ω3＝45

ω4＝50， ωc＝13，H＝11.25

③将∣G0Gc∣（dB）与∣G0∣（dB）特性相减，得串联校正装置传递函数

④校正后系统开环传递函数

验算性能指标，经计算：ωc＝13，γ＝45.6°，Mr＝1.4，σ％＝32％，ts＝0.73（s），满足设计要求。

例6-7 设2型系统的开环传递函数为

试确定使该系统达到下列性能指标的串联校正装置：保持稳态加速度误差系数Ka＝25s﹣2不变，超调量σ≤30％，调整时间ts≤0.9s。

解 ①绘制原系统的近似对数幅频特性曲线，如图6-30中曲线I。

②绘制希望特性。为保持稳态加速度误差系数Ka不变，希望特性的低频段应和图6-30中特性I重合。希望特性的中频段斜率取为﹣20dB/dec，并使它和低频段直接连接。因此它的位置取决于第一个转折频率ω2。

根据σ＝30％的要求，由式（5-88）得Mr＝1.35。

为使ts≤0.9s，由式（5-106），得ωc＝9.9。

由式（6-33）得

由特性Ⅰ上ω＝2.5的A点，画一斜率为﹣20dB/dec的线段，它右端B点处的频率，就是特性Ⅰ的转折频率ω3，将这一线段作为希望特性的中频段。

为使希望特性尽量靠近原系统的特性I，过B点画一条斜率为﹣60dB/dec的直线并延长至图的边缘，该直线即作为希望特性的高频段。

得到如图6-30中折线Ⅱ所示的希望特性。它为2-1-3型的，与典型的2-1-2型的高频部分有区别。希望特性过ω3后，斜率由﹣20dB/dec改变为﹣60dB/dec，说明有两个时间常数为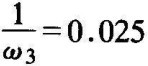的惯性环节。

经验算，按画出的希望特性确定的校正装置能保证系统具有要求的性能。

③图6-30中曲线Ⅱ减曲线∣得校正装置的对数幅频特性曲线Ⅲ。按曲线Ⅲ写出校正装置的传递函数

这是一个超前校正装置的传递函数。

图6-30 例6-7题系统及校正装置的对数幅频渐近线