前面介绍了几种用曲线表示开环系统频率特性的方法，利用这些曲线可以分析系统的稳定性及其他的频域性能指标，还可由开环频率特性求取控制系统的闭环频率特性。利用Matlab工具箱中函数，可以准确地作出系统的频率特性曲线，为控制系统的设计和分析提供了极大的方便。
Matlab工具箱中，绘制系统频率特性曲线的几个常用函数有bode，nyquist，nichols， ngrid，margin等，下面通过具体的例子来说明这些函数的应用。
（1）函数bode
函数bode可以求出系统的Bode图，其格式为
[mag，phase，w]＝bode（num，den）
[mag，phase，w]＝bode（num，den，w）
bode（num，den）可以绘制传递函数为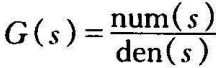
时系统的Bode图。
bode（num，den，w）可利用指定的频率值ω绘制系统的Bode图。
当带输出变量引用函数时，可以得到系统Bode图相应的幅值、相角及频率值。其中
mag＝∣G（jω）∣
phase＝∠G（jω）
（2）函数nyquis
函数nyquis的功能是求系统的奈氏曲线，格式为
[re，im，w]＝nyquist（num，den）
[re，im，w]＝nyquist（num，den，w）
nyquist（num，den）可以得到开环传递函数为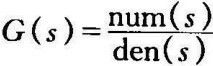
时系统的nyquist曲线。
nyquist（num，den，w）可以根据指定的频率值ω绘制系统的nyquist曲线。
当带输出变量引用函数时，可以得到系统nyquist曲线的数据，而不直接绘出nyquist曲线。
（3）nichols函数
nichols函数可求出系统频率特性的nichols图线，格式为
[mag，phase，w]＝nichols（num，den）
[mag，phase，w]＝nichols（num，den，w）
nichols（num，den）可以得到开环传递函数为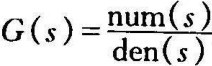
时系统的nichols图线。
nichols（num，den，w）可以根据指定的频率值ω绘制系统的nichols图线。
当带输出变量引用函数时，可以得到系统nichols图线的数据，而不直接绘出nichols图线。
（4）ngrid函数
ngrid函数的功能是绘制nichols图线上的网格。格式为
ngrid
ngrid（‘new’）
ngrid函数可在nichols图线上加网格线，ngrid（‘new’）可在绘制网格前清除原图，然后再设置成hold on，这样，后续的nichols函数可与网格绘制在一起。
（5）margin函数
margin可求出开环系统的幅值裕度和相角裕度，其格式为
margin（num，den）
[gm，pm，wcg，wcp]＝margin（mag，phase，w）
margin（num，den）可计算系统的相角裕度和幅值裕度，并绘制出Bode图。
margin（mag phase，w）可以由幅值裕度和相角裕度绘制出Bode图，其中，mag，phase和w是由bode得到的幅值裕度、相角裕度和频率。
当带输出变量引用函数时，仅计算幅值裕度、相角裕度及幅值穿越频率wcg和相角穿越频率wcp，不绘制Bode图。
例5-13 二阶振荡环节的传递函数为
绘制ζ取不同值时的Bode图。
解 取ωn＝8，取[0.1∶0.2∶1.0]，由bode函数得到Bode图，Matlab程序如下
％example 5-13
％
wn＝8；
kosi＝[0.1∶0.2∶1.0]；
w＝logspace（﹣1，1，100）；
figure（1）
num＝[ωn.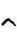
2]；
for kos＝kosi
den＝[12*kos*wn wn.
2]；
[mag，pha，w1]＝bode（num，den，w）；
subplot（2，1，1）；hold on
semilogx（w1，mag）；(www.xing528.com)
subplot（2，1，2）；hold on
semilogx（w1，pha）；
end
subplot（2，1，1）；grid on
title（‘Bode Plot’）；
xlabel（‘Frequency（rad/sec）’）；
ylabel（‘Gain dB’）；
subplot（2，1，2）；grid on
xlabel（‘Frequency（rad/sec）’）；
ylabel（‘Phase deg’）；
hold off
程序执行后，得到二阶振荡环节的Bode图如图5-63所示。
例5-14 开环系统的传递函数为
①绘制系统的奈氏曲线，并用奈氏判据判断系统的稳定性；
②求闭环系统的单位脉冲响应。
解 利用nyquist函数绘制奈氏曲线如图5-64所示。由图可知，奈氏曲线不围绕（﹣1，j0）点，N＝0，开环传递函数有一个右半S平面的极点，P＝1，由奈氏判据
Z＝P－N＝1
系统不稳定。又由系统的脉冲响应曲线图5-65，可知脉冲响应是发散的，也说明系统不稳定。
图5-63 二阶振荡环节的Bode图
图5-64 系统的奈氏曲线
图5-65 系统的单位脉冲响应
Matlab程序如下
％example 5-14
％
k＝30；
z＝[1]；
p＝[﹣2－32]；
[num，den]＝zp2tf（z，p，k）；
figure（1）
nyquist（num，den）
title（‘Nyquist Plot’）；
figure（2）
[numl，denl]＝cloop（num，den）；
impulse（num，den）
title（‘Impulse Response’）
例5-15 系统的开环传递函数为
绘制Nichols图。
解 Matlab程序如下
％example 5-15
％
k＝16.7/0.0125；
z＝[0]；
p＝[﹣1.25－4 －16]；
[num，den]＝zp2tf（z，p，k）；
figure（1）
ngrid（‘new’）
nichols（num，den）
title（‘Nichols Plot’）
程序执行后，可得到系统的Nichols图如图5-66所示。
图5-66 系统的Nichols图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
