闭环系统频域性能指标优化方法

（1）闭环频率特性指标

典型闭环幅频特性如图5-60所示，特性曲线随着频率ω变化的特征可用下述一些特征量加以概括：

①闭环幅频特性的零频值A（0）；

②谐振频率ωr和谐振峰值；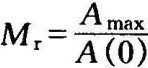

③带宽频率ωb和系统带宽（0～ωb）。

（2）频域指标与时域指标的关系

频域响应和时域响应都是描述控制系统固有特性的方法，因此两者之间必然存在某种内在联系，这种联系通常体现在控制系统频率特性的某些特征量与时域性能指标之间的关系上。

图5-60 典型闭环幅频特性

①闭环幅频特性零频值A（0）与系统无差度v之间的关系。

单位反馈系统的开环传递函数可写成下列形式

令

则

式中 K——系统的开环放大系数；

v——系统的无差度，即开环传递函数G（s）中积分环节的个数；

G0（s）——开环传递函数G（s）中除开环放大系数K和积分项以外的表达式，它满足

用s＝jω代入式（5-84）得到系统的开环频率特性为

对于单位反馈系统，闭环频率特性为

即

由此得到系统闭环幅频特性的零频值是

其中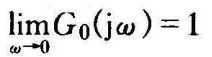

当系统无差度v＞0时，由式（5-86）得

A（0）＝1

当系统无差度v＝0时，由式（5-86）得

综上分析，对于无差度v≥1的无差系统，闭环幅频特性的零频值A（0）＝1；而对于无差度v＝0的有关系统，闭环幅频率特性的零频值A（0）＜1。式（5-87）说明，系统开环放大系数K越大，闭环幅频特性的零频值A（0）愈接近于1，有差系统的稳态误差将愈小。

②谐振峰值Mr与系统超调量σp的关系。

单位反馈二阶系统的开环传递函数的标准形式为

其对应的闭环频率特性为

由5.2节中式（5-28）知，二阶系统的相对谐振峰值Mr与阻尼比ζ之间的关系为

或写成

对于二阶系统，系统的超调量σp为

图5-61 超调量与谐振峰值的关系曲线(www.xing528.com)

将式（5-90）代入式（5-91）便可得到二阶系统的相对谐振峰值Mr与系统超调量σp之间的关系为

图5-61是由式（5-92）得到的关系曲线，由图可见二阶系统的相对谐振峰值Mr＝1.2～1.5时，对应的系统超调量σp＝20％～30％，这时系统可以获得较为满意的过渡过程。如果Mr＞2，则系统的超调量σp将超过40％。

③谐振频率ωr及系统带宽与时域性能指标的关系。

由5.2节中的式（5-27）知，二阶系统的谐振频率ωr与无阻尼自然振荡频率ωn和阻尼比ζ之间的关系为

由

得到

和

式（5-96）和式（5-97）说明，对于给定的阻尼比ζ，二阶系统的峰值时间tp和调整时间ts均与系统的谐振频率ωr成反比。即谐振频率ωr愈高，系统的反应速度愈快；反之，则系统的反应速度愈慢。所以系统的谐振频率ωr是表征系统响应速度的量。

如图5-60所示，系统的带宽是指系统的幅频特性A（ω）由频率为零的零频值A（0）变化到时所对应的带宽频率ωb的频率变化范围，即0≤ω≤ωb。二阶系统的带宽频率可由下式求出

由此得到带宽频率ωb与无阻尼自然振荡频率ωn及阻尼比ζ的关系为

将式（5-98）等号两边分别乘以式（5-94）和式（5-95）等号两边得到

和

式（5-99）和式（5-100）说明，对于给定的阻尼比ζ，二阶系统的带宽频率ωb与峰值时间tp和调整时间ts也是成反比的。带宽频率ωb愈大，系统的响应速度愈快。所以，由带宽频率ωb决定的系统带宽也是表征系统响应速度的特征量。一般来说，频带宽的系统有利于提高系统的响应速度，但同时容易引入高频噪声，故从抑制噪声的角度来看，系统带宽又不宜过大。因此在设计控制系统时，要恰当处理好这个矛盾，在全面衡量系统性能指标的基础上，选择适当的频带宽度。

④相角裕度γ与阻尼比ζ的关系。

二阶系统的开环频率特性为

由5.4知，系统的幅值穿越频率（又称剪切频率）ωc满足∣G（jωc）∣＝1，因此

即

由此得到

二阶系统的相角裕度是

将式（5-101）代入式（5-102）得到

二阶欠阻尼系统的相角裕度γ与阻尼比ζ之间的关系曲线如图5-62所示。由图5-62可以看出，在阻尼比ζ≤0.7的范围内，它们之间的关系可近似地用一条直线表示，即

ζ≈0.01γ （5-104）

上式表明，选择30°～60°的相角裕度时，对应的系统阻尼比约为0.3～0.6。

图5-62 相角裕度与阻尼比

⑤高阶系统的频域响应和时域响应。

控制系统的频域和时域响应可由傅立叶积分进行变换，即

式中C（t）为系统的被控信号，和R（jω）分别是系统的闭环频率特性和控制信号的频率特性。一般情况下，直接应用式（5-105）求解高阶系统的时域响应是很困难的。在前面的章节中介绍了主导极点的概念，对于具有一对主导极点的高阶系统，可用等效的二阶系统来近似进行分析。实践证明，只要满足主导极点的条件，分析的结果是令人满意的。若高阶系统不存在主导极点，则可采用以下两个近似估算公式来得到频域指标和时域指标的关系：

其中

一般，高阶系统实际的性能指标比用近似公式估算的指标要好，因此，采用近似公式（5-106）和（5-107）对系统进行初步设计，可以保证实际系统满足要求且有一定的余量。