对数频率特性曲线简介

对数频率特性曲线又称对数坐标图或波德（Bode）图，包括对数幅频和对数相频两条曲线。在实际应用中，经常采用这种曲线来表示系统的频率特性。

对数幅频特性曲线的横坐标是频率ω，按对数分度，单位是rad/s。纵坐标表示对数幅频特性的函数值，采用线性分度，单位是dB。对数幅频特性用L（ω）表示，定义如下

L（ω）＝201g∣G（jω）∣

对数相频特性曲线的横坐标也是频率ω，按对数分度，单位是rad/s。纵坐标表示相频特性的函数值，记作φ（ω），单位是度。采用对数分度的横轴如图5-19所示。

图5-19 对数分度和线性分度

由于 ω＝1，lgω＝0

ω＝10，lgω＝1

ω＝100，lgω＝2

⋯⋯

所以，频率ω每扩大十倍，对应横轴上变化一个单位长度，故对ω而言，坐标分度是不均匀的，对lgω则是均匀分度的。

采用对数座标有以下特点：

①在求幅频特性时，可以将各环节幅值相乘转化为幅值相加；

②可以采用渐近线的方法，用直线段画出近似的对数幅频特性曲线；

③对于最小相位系统，可以由对数幅频特性曲线得到系统的传递函数。

另一种采用对数坐标表示系统频率特性的曲线是对数幅相曲线（又称尼柯尔斯曲线），用一条曲线表示相频特性和对数幅频特性，横坐标和纵坐标都是线性分度的。横坐标表示相角，纵坐标表示对数幅频特性的分贝数，都是以频率ω为参变量。以惯性环节为例，其对数幅相曲线如图5-20所示。

（1）典型环节的对数频率特性

首先讨论典型环节的对数频率特性曲线，再讨论由这些典型环节构成的开环系统的对数频率特性曲线的画法及其特点。

a.比例环节比例环节的频率特性

G（jω）＝K

由于其幅值和相角都不随ω变化，所以，对数幅频特性曲线是一条与0dB线平行且距0dB线为20lgK的直线。K＞1时，20lgK＞0，直线在0dB线之上，K＜1时，20lgK＜0直线在0dB线之下。对数相频特性为0°，Bode图如图5-21所示。

图5-20 惯性环节的对数幅相曲线

图5-21 比例环节的对数频率特性曲线

b.积分环节 由式（5-17），求得积分环节的对数幅频特性为

在Bode图上，是一条在ω＝1处穿过横轴的直线，直线的斜率可由下式求出

式（5-36）表明，频率变化10倍，则对数幅值下降﹣20dB，故直线的斜率为﹣20dB/dec。相频特性是﹣90°且平行于横轴的直线，如图5-22所示。

图5-22 积分环节的对数频率特性曲线

图5-23 v个积分环节的对数频率特性

若有v个积分环节串联，则其对数幅频特性为

相频特性为

（5-37）式表明，v个积分环节串联的对数幅频特性曲线是在ω＝1处穿过横轴的直线，直线的斜率为﹣v×20dB/dec。相频特性曲线是﹣v×90°且平行于横轴的直线，如图5-23所示。

c.惯性环节惯性环节的对数幅频特性为

在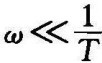的低频段，即ωT1，则幅频特性可近似为

故在低频段，幅频特性是与横轴重合的直线。在的频段内，对数幅频特性可近似为

这是一条在处穿越横轴，斜率为﹣20dB/dec的直线。由以上分析不难得出，低频段与高频段的两条直线在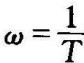处相交。用渐近线来表示对数幅频特性，当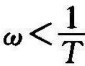时，幅频特性由0dB直线近似，时，幅频特性由斜率为﹣20dB/dec的直线近似，频率称幅频特性曲线的转折频率，由这两条线段构成惯性环节的近似对数幅频特性。显然，在频率为时，曲线的误差最大，误差为

在频段内的误差见表5-1。

表5-1 惯性环节渐近幅频特性误差表

由表5-1可看到，在频率和处，幅值的精确值与近似值间的误差为-0.04dB，在频段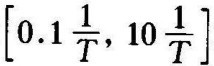之外的误差更小。所以，若要获取较精确的幅频特性曲线，只需在频段内对渐近特性进行修正即可。

惯性环节的相频特性可根据φ（ω）＝﹣arctanωT 绘制。ω＝0时，φ（ω）＝0°，ω＝∞时，φ（ω）＝﹣90°，在转折频率处，φ（ω）＝﹣45°，惯性环节相频特性数据见表5-2。对数相频特性曲线关于点，φ（ω）＝﹣45°斜对称。惯性环节的Bode图如图5-24所示。

表5-2 惯性环节的相频特性数据

惯性环节的转折频率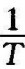减小或增大，相频特性曲线和幅频特性曲线相应地左移或右移，但其形状不变。

图5-24 惯性环节的对数频率特性曲线

图5-25 振荡环节的渐近对数幅频特性

d.振荡环节

由振荡环节的频率特性，得到其对数幅频特性为

由对数频率特性表达式可看出，在频率的低频段，对数频率特性可近似为

这表明在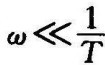的频段内，对数幅频特性是与横轴重合的直线段。

在频率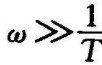的高频段内，频率特性可近似为

这是一条在过零分贝线，斜率为﹣40dB/dec的直线段。以上两条直线在转折频率处相交，它们构成振荡环节的渐近对数幅频特性。如图5-25所示。

若分别用L（ω），La（ω）和△L表示振荡环节对数幅频特性的精确值、近似值及它们之间的误差值，则有

△L＝L（ω）－La（ω）（5-44）

图5-26 振荡环节的幅频特性的误差曲线

由式（5-45）和式（5-46）知，振荡环节的渐近幅频特性曲线与精确曲线间的误差是频率ω和阻尼比ζ的函数。由△L的表达式可绘制误差曲线如图5-26所示。由振荡环节的相频特性可绘制对数相频特性曲线如图5-27所示。由于相频特性也是频率ω和阻尼比ζ的函数，所以曲线形状随着ζ取值的不同而异，但都是在频率处通过﹣90°，且曲线在这点关于﹣90°线斜对称。

图5-27 振荡环节的相频特性曲线

e.一阶微分环节由一阶微分环节的频率特性可求得对数幅频特性为

与惯性环节的分析方法类似，可得到在频率和两个频段内，用两条直线来表示一阶微分环节的渐近对数幅频特性。在频率的频段内，渐近特性是与0dB线重合的直线，在的频段内，是斜率为＋20dB/dec的直线，在转折频率处，精确幅频特性与渐近频率特性之差为3dB。(www.xing528.com)

由一阶微分环节的相频特性φ（ω）＝arctanωτ可绘制出相频特性曲线，相角变化范围是0°～90°。一阶微分环节的Bode图如图5-28所示。将图5-28与图5-24比较可以发现，一阶微分环节的对数频率特性曲线与惯性环节的对数频率特性曲线关于横轴对称。

f.二阶微分环节二阶微分环节的对数幅频特性和相频特性分别为

二阶微分环节的Bode图可仿照振荡环节Bode图的绘制过程作出，如图5-29所示。

将图5-29与图5-25、图5-27比较可知，二阶微分环节的对数频率特性与振荡环节的频率特性关于横轴互为镜像。

图5-28 一阶微分环节的Bode图

图5-29 二阶微分环节的Bode图

g.不稳定环节在典型环节幅相频率特性的讨论中，以惯性环节和不稳定的惯性环节为例，分析了它们的频率特性的特点。下面以不稳定的惯性环节和不稳定的振荡环节为例，说明不稳定环节对数频率特性曲线的特点，并将它们与对应的稳定环节相比较。

不稳定惯性环节的频率特性为

对数幅频特性为

相频特性为

φ（ω）＝﹣（﹣arctanωT）＝arctanωT（5-50）

其对数幅频特性与惯性环节相同，当频率ω从0～∞变化时，相角变化范围是0至90°，如图5-30所示，与图5-24比较可知，不稳定惯性环节的对数幅频特性曲线与惯性环节相同，相频特性曲线与惯性环节关于横轴互为镜像。

不稳定振荡环节的频率特性为

对数幅频特性

相频特性为

比较式（5-51）和式（5-43）知，不稳定振荡环节的对数幅频特性与振荡环节的相同，而它们的相频特性关于横轴对称。由式（5-52）和式（5-53）可知，不稳定振荡环节的相角变化范围是0°～180°，Bode图如图5-31所示。

图5-30 不稳定惯性环节的Bode图

①—不稳定惯性环节；②—稳定惯性环节

图5-31 不稳定振荡环节的Bode图

①—不稳定振荡环节；②—稳定振荡环节

（2）开环系统的对数频率特性曲线

掌握了典型环节的对数频率特性曲线的画法，可以很方便地绘制开环系统的对数频率特性曲线（Bode图）。

设开环系统由n个典型环节串联组成，这些环节的传递函数分别为G1（s），G2（s），，Gn（s），则系统的开环传递函数为

其对数幅频特性为

相频特性为

式（5-54）和式（5-55）表明由n个典型环节串联组成的开环系统的对数幅频特性曲线和对数相频特性曲线可由各典型环节相应的曲线叠加得到。

例5-6 已知控制系统的开环传递函数为

试绘制系统Bode图。

解 开环系统由比例、积分、惯性、一阶微分和振荡环节组成，对数幅频特性和对数相频特性分别为

开环系统有三个转折频率，分别是ω1＝0.5，ω2＝2，ω3＝8，首先分析在不同的频率范围内，L（ω）的渐近特性。

①在ω≤ω1的频率范围内，L1和L2为正值，L3＝L4＝L5＝0，ω＝ω1时， L1（ω1）＝12dB，L2（ω1）＝6dB，L2（ω）的斜率为﹣20dB/dec，故在ω≤ω1的频段内， L（ω）是一条在ω＝ω1处幅值为18dB，斜率为﹣20dB/dec的直线。

②在ω1＜ω＜ω2的频率范围内，L3（ω）≠0，斜率为﹣20dB/dec，叠加后的L（ω）是一条斜率为﹣40dB/dec，在ω2处幅值为﹣6dB的直线。

③在ω2＜ω＜ω3的频率范围内，L4（ω）≠0，其斜率为＋20dB/dec因此叠加后的L （ω）是一条斜率为﹣20dB/dec，在频率ω3处幅值为﹣18dB的直线。

④在ω＞ω3的频率范围内，L5（ω）的斜率为﹣40dB/dec，故L（ω）的斜率为﹣60dB/dec。

根据以上分析，各画出L（ω）的渐近特性如图5-32（a）中实线所示。

对数相频特性曲线可分别将积分环节、惯性环节、微分环节和振荡环节的相频特性曲线画出，惯性环节和微分环节可根据表5-2，确定几个点，再用曲线板连起来即可，振荡环节可根据图5-27和ζ的值确定几点，再连接成光滑的曲线。将各环节的相频特性曲线叠加起来，就可得到开环系统的对数相频特性如图5-32（b）所示。

最小相位系统的幅频特性曲线与相频特性曲线有一定的关系，当幅频特性曲线的负斜率加大时，相频特性曲线的负相角也增加，若φ（ω）向正相角方向变化，则对应的幅频特性曲线也向斜率增加的方向变化。因此，用Bode图分析最小相位系统时，只用画对数幅频特性曲线就可以了。L（ω）的渐近线是由一些直线段组成的。L（ω）曲线由低频段向高频段延伸时，每经过一个转折频率，直线段的斜率就相应的改变一次。经过一个比例微分环节，转折频率增加20dB/dec，经过一个惯性环节，转折频率增加﹣20dB/dec，经过一个振荡环节，转折频率增加﹣40dB/dec，按照这些规律，可以一次画成L（ω）的渐近线。具体画法步骤是：

①求出比例微分、惯性环节和振荡环节的转折频率，并将它们标在Bode图的ω轴上，

②确定L（ω）渐近线起始段的斜率和位置。在L（ω）的起始段，ω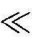1，则

根据式（5-56）右端的第二项，可以确定渐近线起始段的斜率为﹣v×20dB/dec，第一项确定了在ω＝1时，渐近线起始段的高度为20lgK。因此，过ω＝1，L（ω）＝20lgK这一点画一条斜率为﹣v×20dB/dec的直线，该直线从低频段开始向高频段延伸，直至第一个转折频率处，该条直线就是L（ω）渐近线的起始段。

图5-32 例5-6题系统对数频率特性曲线

③将L（ω）向高频段延伸，且每过一个转折频率，将渐近线的斜率相应的改变一次，就可得到L（ω）的渐近线。

例5-7 绘制下面开环系统频率特性的对数幅频特性曲线

解首先作出L（ω）的渐近线，再画出精确曲线。

确定有关环节的转折频率

惯性环节1 ω1＝1rad/s

微分环节 ω2＝1/0.4＝2.5rad/s

惯性环节2 ω3＝1/0.2＝5rad/s

振荡环节 ω4＝1/0.04＝25rad/s

确定L（ω）起始段的高度及斜率。因为v＝1，渐近线起始段的斜率为﹣20dB/dec，在ω＝1时，起始线段的高度为20lg10＝20dB。过ω＝1和L（ω）＝20dB一点向低频段画斜率为﹣20dB/dec的直线。

将直线向高频段延伸。在ω＝1时，斜率变为﹣40dB/dec；在ω＝2.5时，斜率应增加20dB/dec，变为﹣20dB/dec；在ω＝5时，斜率改变为﹣40dB/dec；在ω＝25时，斜率变为﹣80db/dec。根据以上讨论，可作出渐近对数幅频特性曲线如图5-33中的实线所示。

当渐近对数幅频特性曲线的幅值穿越频率附近存在转折频率时，由渐近线确定的幅值穿越频率是不准确的，可根据表5-1或图5-26对渐近曲线进行修正，画出精确的对数幅值曲线。

图5-33 例5-7题对数幅频特性曲线