幅相频率特性曲线详解

幅相频率特性曲线简称幅相曲线，又称极坐标图。其特点是以角频率ω作自变量，把幅频特性和相频特性用一条曲线同时表示在复平面上。例如，5.1节中的RC网络，当ω＝1/T 时，幅频特性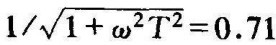，相频特性﹣arctanωT＝45°，幅值和相角在复平面上可用一矢量来表示，矢量的长度为0.71，矢量与实轴正方向的夹角45°（逆时针方向角度为正，顺时针方向角度为负）。当角频率ω从0到∞变化时，可以在复平面上得到一系列这样的矢量，这些矢量的矢端在复平面上描绘出一条曲线，该曲线就是频率特性的幅相曲线。由于幅频特性是角频率ω的偶函数，相频特性是ω的奇函数，所以，ω从0变化到∞时的幅相曲线与ω从﹣∞变化到0的幅相曲线关于实轴对称，通常，只画出ω从0变至∞时的幅相曲线，并在曲线上用箭头表示ω增大的方向。

（1）典型环节的幅相曲线

①典型环节。

通常，控制系统的开环传递函数G（s）H（s）的分子和分母多项式都可以分解成若干因子相乘的形式，如下式表示

式（5-16）描述了由一系列具有不同传递函数的环节串联组成的开环系统的特性，式中的这些环节依次称为比例环节、积分环节、惯性环节、振荡环节、一阶微分环节和二阶微分环节。一般线性系统的开环传递函数大多由这些环节组成，因此，把他们称作典型环节。下面分别讨论这些环节的幅相曲线。

②典型环节的幅相曲线。

a.比例环节 比例环节的频率特性为

G（jω）＝K

幅频特性 ∣G（jω）∣＝K

相频特性∠G（jω）＝0°

可知，比例环节的幅值为常数K，相角为0，它们都不随频率ω变化，故在复平面上，比例环节的幅相曲线为正实轴上的一点，幅相曲线如图5-4所示。

b.积分环节积分环节的频率特性为

由式（5-17）和式（5-18）可知，当频率ω从0变化到∞时，积分环节的幅频特性由∞变化到0，相频特性始终等于﹣90°。积分环节是相角滞后环节，幅相曲线是一条与负虚轴重合的曲线，如图5-5所示。

图5-4 比例环节的幅相曲线

图5-5 积分环节的幅相曲线

c.惯性环节 惯性环节的频率特性为

由式（5-19）知 ω＝0，∣G（jω）∣＝1，∠G（jω）＝0°

所以，ω由0变化到∞时，幅频特性从1变化到0，相频特性由0变化至﹣90°，故幅相曲线从正实轴上距原点为1处开始，顺时针变化，与负虚轴相切进入原点。可以证明，幅相曲线在G（jω）平面上是正实轴下方的半圆。

则有

式（5-23）是一圆方程，圆心在（1/2，0）处，圆半径为1/2。

惯性环节的幅相曲线如图5-6所示。

由图5-6知，惯性环节是一个相位滞后环节，在低频时，滞后相角较小，幅值的衰减也较小，频率越高，滞后相角越大，幅值的衰减也越大，最大的滞后相角为90°。

d.振荡环节振荡环节的频率特性为

振荡环节的幅频特性和相频特性为

图5-6 惯性环节的幅相曲线

图5-7 振荡环节的幅相曲线

由式（5-25）和式（5-26）知，振荡环节的幅频特性和相频特性不仅与频率ω有关，还与阻尼比ζ有关。不同阻尼比时的频率特性曲线如图5-7所示。由图可见，当阻尼比较小时，在某一频率时会产生谐振，谐振时的幅值大于1。称此时的频率为谐振频率ωr，相应的幅值为谐振峰值Mr。ωr和Mr都可以由极值方程得到

可求得

将ωr代入式（5-25），可得

（5-27）式表明，当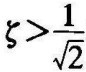时，谐振频率不存在。当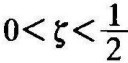时，由式（5-27）知，谐振频率。振荡环节的幅相曲线如图5-7所示。在0＜ω＜ωr的范围内，随ω的增加，∣G（jω）∣逐渐增大，当ω＝ωr时，∣G（jω）∣达到最大值M1，当ω＞ωr时，∣G（jω）∣迅速减小，当幅值衰减至∣G（jω）∣＝0.707时，对应的频率称为截止频率ωc。当频率大于ωc，幅值衰减得很快。振荡环节是相位滞后环节，最大的滞后相角是180°。

e.一阶微分环节一阶微分环节的频率特性为

G（jω）＝jωτ＋1

其中τ为微分时间常数，一阶微分环节的幅频特性和相频特性分别为

幅相频率特性如图5-8所示。它是一条起始于（1，0）点，在实轴上方且与实轴垂直的直线。

图5-8 一阶微分环节的幅相曲线

图5-9 二阶微分环节的幅相曲线

f.二阶微分环节二阶微分环节的频率特性为

G（jω）＝（jω）2τ2＋j2ωτ＋1ζ

幅频特性和相频特性分别为

二阶微分环节的幅相曲线如图5-9所示，它是相位超前环节，最大超前相角为180°。

③不稳定环节。

不稳定环节具有在右半S平面的极点，如传递函数为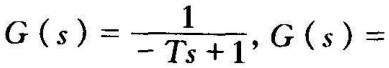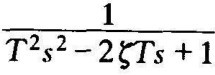的环节就是不稳定环节。这两个环节传递函数的形式分别与惯性环节和振荡环节相似，故称它们为不稳定的惯性环节和不稳定的振荡环节。如传递函数具有﹣Ts＋1，ω2T2－2ζωTs＋1这样的形式，虽不能表明环节不稳定，但按前面不稳定的惯性环节和不稳定的振荡环节的叫法，仍将它们称作不稳定的一阶微分环节和不稳定的二阶微分环节。在第4章中，曾提到非最小相位环节，不稳定环节就属这类环节。这类环节（系统）与只含有左半S平面开环零极点的环节（系统）相比，它们对于正弦信号稳态响应的幅频特性完全相同，而相频特性却有很大差别。下面以惯性环节和不稳定的惯性环节为例，研究它们的频率特性有什么特点。

不稳定惯性环节的频率特性为

幅频特性和相频特性分别为

将式（5-33）和式（5-34）与式（5-20）和式（5-21）相比，可知不稳定惯性环节的幅频特性与惯性环节的幅频特性完全一样，相频特性则不同。不稳定惯性环节当ω从0变化至∞时，相角变化从0至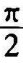，惯性环节的相角变化则从0至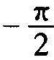。两环节的幅相曲线关于实轴对称，如图5-10所示。

与上面的分析方法类似，可知不稳定振荡环节和其对应的振荡环节的幅频特性相同，相频特性不同。不稳定振荡环节的相角变化范围是0至π，振荡环节的相角范围是0至﹣π，它们的幅相频率特性曲线也对称于实轴，如图5-11所示。

图5-10 不稳定惯性环节的幅相曲线

图5-11 不稳定振荡环节的幅相曲线

（2）开环系统的幅相曲线

前面讨论了构成控制系统的各个环节的幅相频率特性曲线，一般控制系统都可由以上各环节构成，我们掌握了这些环节的幅相频率特性曲线的画法，就不难得到系统的幅相频率特性曲线。在实际应用中，常常通过开环系统的幅相频率特性曲线（简称开环幅相曲线）来分析系统的稳定性。开环幅相曲线可以用解析的方法，给定ω值，计算出对应的幅值和相角，绘制幅相曲线，也可通过分析开环系统的频率特性，画出大致的幅相曲线。下面着重介绍开环幅相曲线的大致画法。

例5-1 系统的开环传递函数为

试概略绘制系统的开环幅相曲线。

解 开环系统由比例环节和两个惯性环节组成，开环频率特性为

幅频特性

相频特性

根据开环系统的幅频特性和相频特性，可以计算出ω＝0和ω＝时的幅值和相角，即得到幅相曲线的起始位置和终点位置。

ω＝0，∣G（jω）H（jω）∣＝K，

∠G（jω）H（jω）＝0°

ω＝∞，∣G（jω）H（jω）∣＝0，

∠G（jω）H（jω）＝﹣180°

由此可知，开环幅相曲线起始于正实轴，至原点的距离为K处，曲线的终点在原点，且与负实轴相切进入原点，相角变化范围是0°～﹣180°。大致的开环幅相曲线如图5-12所示。(www.xing528.com)

图5-12 例5-1题系统幅相曲线

例5-2 控制系统的开环传递函数为

试绘制系统大致的开环幅相曲线。

解 与上例中的系统比较，开环传递函数中增加了一个积分环节，为1型系统。幅相频率特性分别为

可知，相角变化范围为﹣90°～﹣270°，开环幅相曲线起始于负实轴无穷远处，终点在原点，且曲线与正虚轴相切进入原点。

将频率特性写成实部与虚部的形式

分别称Re[G（jω）H（jω）]和Im[G（jω）H（jω）]为开环系统的实频特性和虚频特性。

在起点 Re[G（jω）H（jω）]＝﹣K（T1＋T2）

Im[G（jω）H（jω）]＝﹣∞

求幅相曲线与实轴的交点（该点对于分析系统的稳定性非常重要），可令Im[G（jω） H（jω）]＝0，得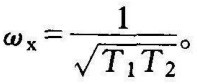

将代入实部，可得

系统的开环幅相曲线如图5-13所示。

若在系统的开环传递函数中再增加一个积分环节，即

则当ω＝0时，∣G（jω）H（jω）∣＝∞，∠G（jω）H（jω）＝－180°，开环幅相曲线起始于负实轴无穷远处，当ω＝∞，∣G（jω）H（jω）∣＝0，∠G（jω）H（jω）＝﹣270°，开环幅相曲线与正实轴相切进入原点，如图5-14所示。

图5-13 例5-2题图（1型系统）

图5-14 例5-2题图（2型系统）

例5-3 系统的开环传递函数为

试绘制概略的开环幅相曲线。

解 系统的开环频率特性为

相频特性为

∠G(jω）H（jω）＝arctanωτ－90°－arctanωT1－arctanωT2

幅频特性为

由频率特性知，开环幅相曲线起始于负虚轴方向的无穷远处，与负实轴相切进入原点。由于系统含有一阶微分环节和惯性环节，其幅相曲线的形状会因时间常数τ，T1，T2的取值不同而异，讨论如下。

将频率特性写成实频和虚频的形式，有

由实频特性可知，ω＝0时，有

Re[G（jω）H（jω）]＝﹣K（T1＋T2－τ）

若T1＋T2＞τ，Re[G（jω）H（jω）]＜0，开环幅相曲线起始于负虚轴左侧的无穷远处；

若T1＋T2＜τ，Re[G（jω）H（jω）]＞0，开环幅相曲线起始于负虚轴右侧的无穷远处；

若T1＋T2＝τ，Re[G（jω）H（jω）]＝0，开环幅相曲线从负虚轴上无穷远处起始。

求曲线与负实轴的交点，令Im[G（jω）H（jω）]＝0，有

若

即

则ω有解，亦即曲线与负实轴有交点。

不等式方程组

无解，故当幅相曲线从负虚轴右侧无穷远起始时，与负实轴无交点，开环幅相曲线如图5-15所示。

图5-15 例5-3题图

例5-4 单位反馈系统的开环传递函数为

试绘制概略的开环幅相曲线。

解 系统的开环频率特性为

幅频特性和相频特性分别为

当ω＝0，∣G（jω）H（jω）∣＝1，∠G（jω）H（jω）＝0°

当ω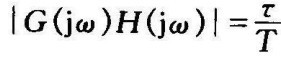＝∞，，∠G（jω）H（jω）＝0°

若τ＞T，arctan ωτ－arctanωT＞0，则幅相曲线在第一象限变化，若τ＜T，则幅相曲线在第四象限内变化，如图5-16所示。

从以上例子可看出，对于开环传递函数只含有左半平面的零点和极点的系统，其幅相曲线的起点和终点具有如下规律（参考图5-17）。

起点：若系统不含有积分环节，曲线起始于正实轴上某点，该点距原点的距离值为开环增益K值；若系统含有积分环节，曲线起始于无穷远处，相角为v×（﹣90°），v为积分环节的个数。

图5-16 例5-4题图

终点：一般，系统开环传递函数分母的阶次总是大于或等于分子的阶次，n＞m时，终点在原点，且以角度（n－m）×（﹣90）°进入原点；n＝m时，曲线终止于正实轴上某点，该点距原点的距离与各环节的时间常数及K等参数有关。

图5-17 开环幅相曲线的起点和终点

若开环传递函数中含有在右半平面的极点或零点，幅相曲线的起点和终点不具有以上规律。对于这样的系统，尤其应注意系统的相频特性。

例5-5 设系统的开环传递函数为

试绘制开环系统的大致幅相曲线。

解 系统的频率特性为

幅相频率特性分别为

幅相曲线如图5-18所示。

图5-18 例5-5题图

曲线与实轴得交点可求取如下

式中U（jω）与V（j）分别为开环系统的实频和虚频特性。

令V（ω）＝0，解得

将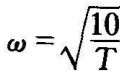代入U（ω），得幅相曲线与实轴得交点为﹣T。