频率特性的概念及其在RC网络中的应用

下面以一个简单的RC网络为例，说明频率特性的概念。图5-1所示的电路，其微分方程为

图5-1 RC电路

令RC＝T，网络的传递函数为

若在网络输入正弦电压，即

er＝Asinωt

则由式（5-1）式有

经拉氏变换，得到电容两端的电压为

式中，第一项为瞬态分量，第二项为稳态分量，当时间趋于无穷时，第一项趋于零，所以

由式（5-2）可知，网络的稳态输出仍然是与输入电压同频率的正弦电压，输出电压的幅值是输入电压的倍，相角比输入迟后了arctanωT弧度。称为RC网络的幅频特性，arctanωT称做相频特性。显然，它们都是频率ω的函数。函数可表示为

它能完整地描述RC网络在正弦函数作用下，稳态输出电压的幅值和相角随输入电压频率ω变化的情况，因此，将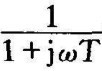称做网络的频率特性。对于任何线性定常系统，都可得到类似的结论。

如图5-2所示任意线性定常系统（闭环或开环系统），设其传递函数为

图5-2 系统框图

输入信号为

R（s）＝Asinωt

其拉氏变换为

系统的传递函数通常可写成

故系统输出的拉氏变换为

经拉氏反变换，可得系统的输出为

对于稳定的系统，由于s1，s2，⋯，sn都具有负实部，所以，当时间趋于无穷时，式（5-3）中的暂态分量都衰减至零，因此，系统输出的稳态分量为

式（5-4）中的b和待定，可由下式计算。(www.xing528.com)

G（jω）是一复数，因此，可用复数的模和相角的形式表示为

同样，G（﹣jω）也可表示为

将式（5-5）、式（5-6）、式（5-7）及式（5-9）代入式（5-3）中，可得

式（5-10）中，C＝∣G（jω）∣A为稳态输出信号的幅值。

式（5-10）表明，线性定常系统对正弦输入信号的稳态响应仍然是与输入信号同频率的正弦信号，输出信号的振幅是输入信号的∣G（jω）∣倍，输出信号相对输入信号的相移为Φ＝∠G（jω），输出信号的振幅及相移都是角频率ω的函数。

G（jω）＝∣G（jω）∣ej∠G（jω）（5-11）

G（jω）称为系统的频率特性，它表明了正弦信号作用下，系统的稳态输出与输入信号的关系。其中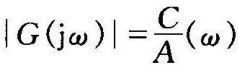为幅频特性，它反映了系统在不同频率的正弦信号作用下，稳态输出的幅值与输入信号幅值之比。为相频特性，它反映了系统在不同频率的正弦信号作用下，输出信号相对输入信号的相移。系统的幅频特性和相频特性统称为系统的频率特性。

比较系统的频率特性和传递函数可知，频率特性与传递函数有如下关系

G（jω）＝G（s）∣s＝jω（5-12）

一般地，若系统具有以下传递函数

系统频率特性可写为

由式（5-12）可推导出线性定常系统的频率特性。对于稳定的系统，可以由实验的方法确定系统的频率特性，即在系统的输入端作用不同频率的正弦信号，在输出端测得相应的稳态输出的幅值和相角，根据幅值比和相位差，就可得到系统的频率特性。对于不稳定的系统，则不能由实验的方法得到系统的频率特性，这是由于系统传递函数中不稳定极点会产生发散或振荡的分量，随时间推移，其瞬态分量不会消失，所以不稳定系统的频率特性是观察不到的。

由频率特性的物理意义可知，当频率ω趋于无穷时，稳态输出的幅值不可能为无穷，故频率特性表达式（5-14）或传递函数表达式（5-13）中，分母多项式的最高次幂n总是大于或等于分子多项式的最高次幂m。

第2章系统的数学模型中，定义线性定常系统的传递函数为在零初始条件下系统输出的拉氏变换与输入的拉氏变换之比

上式的反变换为

若系统稳定，则上式的σ可取为零，如果r（t）的傅氏变换存在，可在式（5-15）中令s＝jω，则有

所以由此可知，稳定系统的频率特性为系统输出的傅氏变换与输入的傅氏变换之比。

系统的频率特性与传递函数、微分方程一样，也能表征系统的运动规律，它是频域中描述系统运动规律的数学模型。这三种数学模型之间存在图5-3所示关系。

图5-3 微分方程、频率特性、传递函数三种数学模型之间的关系