开环零点对根轨迹的影响优化

从下面的例子中，可看到附加开环零点对系统性能的影响。

例4-11 已知系统的开环传递函数为

试用根轨迹法分析系统的稳定性，如果使系统增加一个开环零点，试分析附加开环零点对根轨迹的影响。

解 ①系统的根轨迹如图4-18（a）所示。由于根轨迹全部位于S平面的右半部，所以该系统无论K*取何值，都是不稳定的。

②如果给原系统增加一个负开环实零点z＝﹣b（b＞0），则开环传递函数为

当b＜a时，根轨迹的渐近线与实轴的交点为，它们与实轴正方向的夹角分别为90°和﹣90°，三条根轨迹均在S平面左半部，如图4-18（b）所示。这时，无论K*取何值，系统始终都是稳定的。

当b＞a时，根轨迹的渐近线与实轴的交点为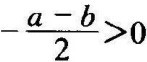，根轨迹如图4-18（c）所示，与原系统相比，虽然根轨迹的形状发生了变化，但仍有两条根轨迹位于S平面的右半部，系统仍不稳定。

图4-18增加开环零点的影响

由以上例子可知，选择合适的开环零点，可使原来不稳定的系统变为稳定的。否则，便达不到预期的目的。

例4-12 系统的开环传递函数为

试分析附加开环零点对系统性能的影响。(www.xing528.com)

解 ①原系统的根轨迹如图4-19（a）所示。由图可知，当系统的根轨迹增益时，由两支根轨迹进入S平面右半部，成为不稳定系统。

②给原系统增加一负实零点z（z＜0），系统的开环传递函数为

根轨迹的渐近线与正实轴的夹角分别为±90°，与实轴的交点坐标位置随附加零点的取值而改变，下面分几种情况加以讨论。

a.当z＜p2＋p3＜0时，渐近线与实轴的交点为

渐近线位于S平面的右半部，根轨迹如图4-19（b）所示。与原系统的根轨迹相比较，虽然根轨迹的形状发生了变化，但仍有根轨迹进入了右半S平面，当时，系统变为不稳定。

b.当p3＜z＜p2＜0时，渐近线与实轴的交点

图4-19 例4-12的根轨迹

渐近线在S平面左半部，根轨迹如图4-19（c）所示由图可知无论根轨迹增益取何值，系统始终是稳定的。

c.当p3＜p2＜z＜0时，渐近线与实轴的交点也小于零，根轨迹如图4-19（d）所示。