理解主导极点的概念与意义

在工程实际中，常常用主导极点的概念对系统进行分析，这样可使系统分析简化。例如研究具有以下闭环传递函数的系统

系统的单位阶跃响应为

h（t）＝1－0.024e﹣10t＋1.55e﹣tcos（t＋129°）

式中，指数项是由闭环极点s1＝﹣10产生的，衰减余弦项是由闭环复数极点s2，3＝﹣1±j产生的，比较这两项可以发现，指数项随时间的增加迅速衰减且幅值很小，故可忽略，所以

h（t）≈1＋1.55e﹣tcos（t＋129°）

上式表明，系统可近似为一个二阶系统，其动态特性可由离虚轴较近的一对闭环极点确定，这样的闭环极点称为闭环主导极点。一般来说，闭环主导极点定义为，在系统的时间响应过程中起主要作用的闭环极点，它们离虚轴的距离小于其他闭环极点的1/5，并且在它附近没有闭环零点。在系统的时间响应过程中，各分量所占的比重除了取决于相应的闭环极点外，还与该极点处的留数，即闭环零、极点间的相互位置有关。故只有既接近虚轴，又不十分接近闭环零点的闭环极点，才可能成为主导极点。在工程计算中，采用主导极点代替系统的全部闭环极点来估算系统性能指标的方法称为主导极点法。

例4-10 已知系统的开环传递函数为

试根据系统的根轨迹分析系统的稳定性并计算闭环主导极点具有阻尼比ζ＝0.5时系统的动态性能指标。

解 ①作根轨迹图。

根轨迹在实轴上的线段为[﹣1，0]，[﹣2，﹣3]。

渐近线与实轴的交点为

渐近线与实轴正方向的夹角为

θa＝±45°和θa＝±135°

由规则5可求出根轨迹在实轴上的分离点为

d1＝﹣0.38，d2＝﹣2.62

由劳斯判据可求得根轨迹与虚轴的交点

令s1的首项系数为零求得K*＝10，将s＝jω和K*＝10代入s2行的辅助方程10s2＋K*＝0，得根轨迹与虚轴的交点为ωc＝±1。根轨迹的大致图形如图4-17所示。

图4-17 例4-10题图

②系统稳定性分析。

由图4-17知，四条根轨迹中有两条从S平面左半部穿过虚轴进入右半S平面，它们与虚轴的交点为ωc＝±1，交点所对应的根轨迹增益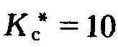，由根轨迹增益与开环增益间的关系有

所以，若使系统稳定，开环增益K的取值应小于1.67。(www.xing528.com)

③动态性能分析。

在根轨迹图上，求出主导极点s1和s2的位置（假定它们满足主导极点的条件）。方法是作ζ＝0.5的等阻尼比线OA，使OA与负实轴方向的夹角为β＝cos－1ζ＝cos－10.5＝60°， OA与根轨迹的交点s1即是满足ζ＝0.5的闭环主导极点之一。由图测得

s1＝﹣0.3＋j0.52

由根轨迹的对称性，可求得另一极点为

s2＝﹣0.3－j0.25

由幅值条件可知，闭环极点s1对应的根轨迹增益为

将s1，s2和代入特征方程，可解得另两个闭环极点为

s3，4＝﹣2.7±j3.37

由于

共轭复数极点s3，4距虚轴的距离是共轭复数极点s1，2距虚轴距离的9倍，且闭环极点s1，2附近无闭环零点，因此，s1，2满足主导极点的条件，该系统可近似成一个由主导极点构成的二阶系统，其闭环传递函数为

此时，对应的系统开环增益为

系统的动态性能可根据二阶系统的性能指标公式计算。

调整时间

超调量

峰值时间

通过该例，可将用根轨迹法分析系统性能的步骤归纳如下。

①根据系统的开环传递函数和绘制根轨迹的基本规则绘制系统的根轨迹图。

②由根轨迹在复平面上的分布分析系统的稳定性。若所有的根轨迹分支都位于S平面的左半部，则说明无论系统的开环增益（或根轨迹增益）取何值，系统始终都是稳定的；若有一条（或一条以上的）根轨迹始终位于S平面的右半部，则系统是不稳定的；若当开环增益在某一范围取值，系统的根轨迹都在S平面左半部，而当开环增益在另一范围取值时，有根轨迹分支进入S平面右半部，则系统为有条件稳定系统，系统根轨迹穿过虚轴，由左半S平面进入右半S平面所对应的K*值，称为临界稳定的根轨迹增益。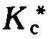

③根据对系统的要求和系统的根轨迹图分析系统的瞬态性能，对于低阶系统，可以很容易地在根轨迹上确定对应参数的闭环极点，对于高阶系统，通常是用简单的作图法求出系统的主导极点（若存在主导极点），然后将高阶系统简化为由主导极点（通常是一对共轭复数极点）决定的二阶系统，来分析系统的性能。这种方法简单、方便、直观，在满足主导极点的条件下，分析结果的误差很小。如果求出的离虚轴最近的闭环极点不满足主导极点的条件，还应考虑其他极点和闭环零点的影响。