非最小相位系统根轨迹优化

若系统的开环传递函数在右半S平面有零点或极点，则该系统称为非最小相位系统。之所以称“非最小相位系统”，是出自这类系统在正弦信号作用下的相移特性（见第5章内容）。

设某负反馈系统的开环传递函数为

由于系统存在一个在S右半平面的开环极点，所以该系统是非最小相位系统。

系统的特征方程为

即有

由式（4-58）知，该系统的根轨迹方程与正反馈系统的一样，其幅值条件和相角条件分别为

因此，应根据0°根轨迹的规则绘制该非最小相位系统的根轨迹。但是，并不是所有非最小相位系统的根轨迹都是按照0°根轨迹的规则画，应根据系统的特征方程来确定。首先，将非最小相位系统的开环传递函数写成式（4-5）的标准形式，使其分子和分母中s的最高次幂的系数为正，此时，若有负号提取出，则按0°根轨迹的规则作图，否则，仍按180°根轨迹的规则作图。下面两个例子说明了非最小相位系统根轨迹的画法。

例4-8 设负反馈系统的开环传递函数为

试绘制系统的根轨迹。

解系统存在一个在右半S平面的开环零点，故该系统为非最小相位系统。将系统的开环传递函数写成式（4-5）的标准形式，有

其根轨迹方程为

亦即

由上式可知，该系统的根轨迹方程与正反馈系统根轨迹方程的形式一样，因此，应按0°根轨迹的规则作图。

由标准形式的开环传递函数可求出系统的两个开环零点为z1＝1，z2＝﹣3，开环极点为p1＝0，。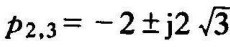

由0°根轨迹的画法规则可知，实轴上的根轨迹为[0，﹣3]，[1，∞）。

渐近线与实轴正方向的夹角为0°，因为渐近线与实轴相交，故渐近线与实轴重合。

由分离点方程

解得d＝3.6。

在两个复数极点处，根轨迹的起始角为

θp2＝0°＋∠（p2－z1）＋∠（p2－z2）－∠（p2－p1）－∠（p2－p3）＝0°＋73.8°＋130.9°－120°－90°＝﹣5.3°

θp3＝5.3°

求根轨迹与虚轴的交点。将s＝jω代入特征方程，并令其实部和虚部分别为零，有

得到方程组

﹣（4－K*）ω2＋3K*＝0

﹣ω3＋（16－2K*）ω＝0

解得ω1＝0，ω2＝±3.14。(www.xing528.com)

根据以上所求，作出根轨迹如图4-15所示。

本例说明，对于非最小相位系统，先应将系统的开环传递函数化为式（4-5）的标准形式，若此时系统的根轨迹方程与正反馈系统相同，即为G（s）H（s）＝1，则按0°根轨迹规则画图，若与负反馈系统相同，即为G（s）H（s）＝﹣1，则按180°根轨迹规则画图。

图4-15 例4-8题根轨迹图

例4-9 具有自动驾驶仪的飞机在纵向运动中的开环传递函数可简化为

试绘制系统的根轨迹，并求使系统稳定的K*的取值范围。

解 实轴上的根轨迹位于[0，1]，[﹣1，﹣∞）。

根轨迹有三条渐近线，它们与实轴的交点为

渐近线与实轴正方向的夹角为

由求根轨迹分离点的公式有

化简得

3d4＋10d3＋21d2＋24d－16＝0

用试探法，可求得上面方程的两个实数根为d1＝0.46，d2＝﹣2.22，用长除法可求得另外两个根为d3，4＝﹣0.79±j2.16，两个复数根不满足幅值条件，舍去。所以，根轨迹在实轴上的分离点为0.46和﹣2.22。

根据劳斯判据，可以求出根轨迹与虚轴的交点。系统的特征方程为

s4＋3s3＋12s2＋（K*－16）s＋K*＝0

劳斯表如下

图4-16 例4-9题根轨迹图

令s1行的第﹣个系数为零，解得K*值为

由s2行得到辅助方程

解辅助方程可得到根轨迹与虚轴的交点

s＝±j2.56 （K*＝35.7）

s＝±j1.56 （K*＝23.3）

求在复数极点处的根轨迹的起始角。对于开环极点，起始角为

θ＝180°＋106°－120°－130.5°－90°＝﹣54.5°

在开环极点处，起始角为θ＝54.5°。

系统的根轨迹如图4-16所示。由根轨迹可知，当23.3＜K*＜35.7时，系统稳定，当K*值超出这一范围时，系统不稳定。