使用非K*作为变参数的根轨迹探析

除了开环增益K以外，还常常分析系统其他参数变化时，对系统性能的影响，比如某环节的时间常数等。绘制这类参数变化时的根轨迹的方法与前面讨论的规则相同，但在绘制根轨迹之前，要先求出系统的等效开环传递函数。

设系统的闭环特征方程为

则系统的闭环特征方程为

1＋G（s）H（s）＝N（s）＋KM（s）＝0（4-42）

将方程左端展开成多项式，用不含待讨论参数的各项除方程两端，得到

式（4-43）中的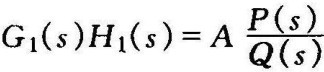即是系统的等效开环传递函数，等效是指系统的特征方程相同意义下的等效。根据等效开环传递函数G1（s）H1（s），按照4-2节介绍的根轨迹绘制规则，就可绘制出以A为变量的参数根轨迹。由等效开环传递函数描述的系统与原系统有相同的闭环极点，但闭环零点不一定相同。因为系统的动态性能不仅与闭环极点有关，还与闭环零点有关，所以在分析系统性能时，可采用由等效系统的根轨迹得到的闭环极点和原系统的闭环零点来对系统进行分析。

例4-5 已知负反馈系统的开环传递函数为，试绘制以T为参变量的根轨迹图。

解 系统的闭环特征方程为

1＋G（s）H（s）＝Ts2（s＋2）＋s2＋2s＋2＝0

①求等效开环传递函数。以不含T的各项除方程两边，得

系统的等效开环传递函数为

②有两个z＝0的零点和一个z＝﹣2的零点，极点为p1＝﹣1＋j，p2＝﹣1－j。

图4-12 例4-5根轨迹图

③实轴上的根轨迹位于﹣∞～﹣2之间。

④从复数极点起始的相角为

θp1＝180°＋45°＋135°＋135°－90°＝45°

θp2＝180°－45°－135°－135°＋90°＝﹣45°

进入原点的终止角为

以T为参变量的系统根轨迹如图4-12所示。(www.xing528.com)

例4-6 设负反馈系统前向通道的传递函数为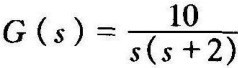，若采用测速反馈H（s）＝1＋Kss，试画出以Ks为参变量的根轨迹。

解 系统的开环传递函数为

系统的特征方程为

s2＋2s＋10Kss＋10＝0

以不含Ks的各项除方程两边，可得

等效开环传递函数为

图4-13 例4-6根轨迹图

开环极点为﹣1±j3，开环零点为0。

实轴上的根轨迹为负虚轴。

求根轨迹的分离点

解得

将d＝﹣3.16代入特征方程，得

（﹣3.16）2＋2×（﹣3.16）＋10Ks×（﹣3.16）＋10＝0

求得Ks值为

Ks＝0.432

求根轨迹的起始角θ

θ＝180°＋108.4°－90°＝198.4°

以Ks为参变量的根轨迹如图4-13所示。