控制系统根轨迹绘制方法

上一节讨论了绘制根轨迹的7条基本规则，按照这些规则，就可粗略地绘制出控制系统根轨迹的大致形状。在此基础上，可在感兴趣的区域内，利用幅值条件和相角条件对根轨迹进行修正，得到该区域内根轨迹的精确图形。

例4-1 闭环系统的特征方程为s（s＋5）（s＋6）（s2＋2s＋2）＋K*（s＋3）＝0，试绘制系统的根轨迹图。

解 系统的开环传递函数为

按照以下步骤绘制根轨迹。

①系统的特征方程为5阶，故根轨迹有5支。根轨迹的起点有5个，p1＝0，p2＝﹣5， p3＝﹣6，p4＝﹣1＋j，p5＝﹣1－j。根轨迹的有限终点为﹣3，有四个无穷远终点。

②有四条根轨迹趋于无穷远处，故有四条渐近线。渐近线与实轴的夹角为

得φa1＝45°，φa2＝﹣45°，φa3＝135°，φa4＝﹣135°。

渐近线与实轴的交点可根据式（4-14）计算，

③实轴上的根轨迹位于0～﹣3及﹣5～﹣6之间。

④根轨迹离开复数极点﹣1＋j的起始角为

θp3＝180°＋[∠（s＋3）－∠s－∠（s＋1＋j）－∠（s＋5）－∠（s＋6）]＝180°＋（26.6°－135°－90°－14°－11.4°）＝﹣43.8°

⑤按式（4-25）求根轨迹的分离点

方程（4-35）是一高阶代数方程，经分析知根轨迹在实轴上只有一个分离点，用试探法求得分离点为d＝﹣5.53。

⑥根轨迹与虚轴的交点可利用劳斯判据确定。由特征方程可列劳斯表如下

若系统稳定，由劳斯表的第一列系数，有以下不等式成立

65.6－0.212K *＞0，3940－105K *－0.163K *2＞0 和 K *＞0

得

0＜K *＜35.6

由此可知，当K *＝35.6时，系统临界稳定，此时，根轨迹穿过虚轴。

K *＝35.6时的ω值由以下辅助方程确定

（65.6－0.212K *）s2＋3K *＝0（4-36）

将K *＝35.6代入辅助方程（4-36），得

58.2s2＋107＝0

解得

s＝±j1.35

由以上步骤，可绘出根轨迹如图4-5所示。

例4-2 闭环系统的特征方程为s（s＋4）（s2＋4s＋20）＋K *＝0，绘制控制系统的大致根轨迹。

解 系统的开环传递函数为

开环极点为

p1＝0， p2＝﹣4， p3＝﹣2＋j4， P4＝﹣2－j4

图4-5 例4-1题根轨迹

实轴上的根轨迹位于0～﹣4之间。

由式（4-25）可知，分离点方程为

d3＋6s2＋18s＋20＝0

解得

d1＝﹣2，d2＝﹣2＋j2.45，d3＝﹣2－j2.45

渐近线与实轴的交点为

渐近线与实轴的夹角为

得

φa1＝45°，φa2＝﹣45°，φa3＝135°，φa4＝﹣135°

令s＝jω代入特征方程得

jω（jω＋4）[（jω）2＋4jω＋20]＋K *＝ω4－36ω2＋K *＋jω（﹣8ω2＋80）＝0

令上式实部和虚部分别为零，有

ω4－36ω2＋K *＝0（4-37）

ω（﹣8ω2＋80）＝0（4-38）

联立解式（4-37）、式（4-38）得

将ω＝3.16代入式（4-37），得到相应的K *值

K *＝260

系统的根轨迹如图4-6所示。

图4-6 例4-2根轨迹

例4-3 已知负反馈系统的特征方程为s3＋as2＋k*s＋k*＝0，研究以k*为参变量，a取几个特殊值时系统的根轨迹。

①当a＝10和a＝3时的根轨迹；

②确定使根轨迹上仅有一个非零值分离点时a的数值。(www.xing528.com)

解 ①当a＝10，系统的开环传递函数为

3个开环极点为p1＝0，p2＝0，p3＝﹣10，有限的开环零点为z＝﹣1。

实轴上的根轨迹位于﹣1～﹣10之间。

渐近线与实轴的交点

渐近线与实轴的夹角

求分离点

解方程得d1＝﹣4，d2＝﹣2.5。

系统的根轨迹如图4-7（a）所示。

图4-7 例4-3根轨迹

当a＝3，系统的开环传递函数为

3个开环极点为p1＝0，p2＝0，p3＝﹣3，有限的开环零点为z＝﹣1。

渐近线与实轴的交点

渐近线与实轴的夹角

求分离点。由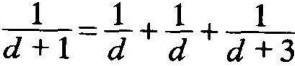，有 d2＋3d＋3＝0

解方程，得

解为复数，故根轨迹在实轴上无分离点。由分析知，d1和d2应舍去。

系统的根轨迹如图4-7（b）所示。

②求仅有一个分离点时的a值，即求方程2d2＋（a＋3）d＋2a＝0有重根时的a值。

若方程有重根，则有（a＋3）2－16a＝0，即a＝1或a＝9。当a＝1时，开环传递函数出现零极点对消，故a＝9为所求。a＝9时的根轨迹如图4-7（c）所示。

例4-4 设系统的开环传递函数为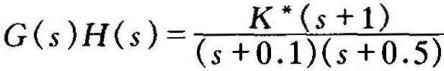，试绘制系统的根轨迹，并证明复平面上的根轨迹是圆。

解根轨迹有两条分支。起点为p1＝﹣0.1，p2＝﹣0.5，有限终点为z1＝﹣1。

实轴上的根轨迹为﹣0.1～﹣0.5，﹣1～﹣∞。

由式（4-25）知，分离点方程为 d2＋2d＋0.55＝0

解得根轨迹在实轴上的分离点为d1＝﹣1.67，d2＝﹣0.33

设s点在根轨迹上，则应满足相角条件

∠（s＋1）－∠（s＋0.1）－∠（s＋0.5）＝180°

将s＝σ＋jω代入上式有

∠（σ＋1＋jω）－∠（σ＋0.1＋jω）－∠（σ＋0.5＋jω）＝180°

即

有

两边取正切，有

整理得 （σ＋1）2＋ω2＝0.672

上式为一圆方程，圆心位于（﹣1，0），圆半径r＝0.67，圆与实轴的交点就是两个分离点。根轨迹如图4-8所示。

关于绘制根轨迹的几点说明。

①闭环极点相同而闭环零点不同的系统，它们的根轨迹可能相同，但其瞬态响应是不同的。

②开环零、极点位置微小的变化可能引起根轨迹形状较大的变化。

图4-9（a）是某系统的根轨迹，当开环零点右移，根轨迹的形状发生了较大变化，如图4-9（b）所示。

图4-8 例4-4 根轨迹

③当G（s）与H（s）有公因子相约时，根轨迹不能代表系统特征方程的全部根，要将G（s）与H（s）中抵消掉的极点加到由根轨迹得到的闭环极点中去。

如图4-10所示控制系统，其闭环传递函数为

系统的特征方程为

D（s）＝（s＋2）[s（s＋3）＋K]（4-39）

图4-9 零极点位置微小的变化引起根轨迹形状的较大变化

若求系统的开环传递函数

则有

1＋G（s）H（s）＝0

得

s（s＋3）＋K ＝0

与式（4-39）比较知，丢掉了s＝﹣2这一极点，而（s＋2）正是G（s）H（s）中抵消掉的公因子。所以，根据式（4-40）得到的根轨迹只能代表图4-11所示结构图的虚线以左的部分，而应将s＝﹣2这一极点增加到系统中去，如图4-11所示。

图4-10 控制系统结构

图4-11 控制系统结构