深入了解根轨迹的基本概念

为了说明根轨迹的基本概念，以图4-1所示系统为例，分析系统参数K从0变化到无穷大时，闭环系统特征方程的根在复平面上变化的情况。

图4-1 控制系统

由图4-1可知，系统的闭环传递函数为

闭环特征方程为

s2＋2s＋K＝0

求解方程可得到系统特征方程的根（系统的闭环极点）为

这表明，特征根是随K值的改变而变化的。下面分析当增益K从0到∞变化时，特征方程的根在S平面上移动的轨迹。K＝0时，s1＝0，s2＝﹣2，这时，系统的闭环极点与系统的开环极点相同。将这两个根用符号“×”在S平面上标注出来，如图4-2所示。以后，用符号“×”表示K＝0时特征方程的根，即开环极点。用符号“〇”表示系统的开环零点。当0＜K＜1时，两个极点s1和s2都是负实数极点，且随K值的增大，s1减小，s2增大，s1从原点开始沿负实轴向左移动，s2从﹣2开始沿负实轴向右移动。因此，从原点0到（﹣2，j0）点这段负实轴是根轨迹的一部分。这时，系统处于过阻尼状态，其阶跃响应是非周期的。当K＝1时，s1＝s2＝﹣1，特征方程有两个重实根。这时系统处于临界阻尼状态，其阶跃响应仍然是非周期的。当K＞1时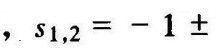，特征方程有两个共轭复数根，其实部为﹣1，不随k值变化，虚部的数值则随K值的增大而变化。s1从（﹣1， j0）开始沿直线向上移动，s2从（﹣1，j0）开始沿直线向下移动，当K从零变化到无穷时，闭环特征方程的根在复平面上的移动的轨迹如图4-2所示。图中，粗实线表示了所有K值时特征方程根在复平面上的轨迹，轨迹是以K为参量画出来的，直线的箭头表示当K值增大时，特征根移动的方向。

图4-2 图4-1所示系统的根轨迹

图4-2所示的根轨迹是由解析的方法得到的，对于阶次较高的系统，这种方法是非常繁琐的。下面通过对闭环系统特征方程的分析，得到求解特征根的作图方法。

控制系统如图4-3所示。它的闭环传递函数为

图4-3 控制系统结构图(www.xing528.com)

闭环特征方程为

1＋G（s）H（s）＝0（4-2）

或写成 G（s）H（s）＝﹣1（4-3）

设系统的开环传递函数有如下形式

或写成

式（4-4）中的K是系统的开环增益。式（4-5）中的zj和pi分别是开环传递函数的零点和极点，K*是将分子和分母分别写成因子相乘的形式，提取的系数，称作根轨迹增益，它与系统开环增益的关系为

将特征方程写成如下形式

称式（4-7）为根轨迹方程，它是一复数方程，由于复数方程两边的幅值和相角应分别相等，因此可将式（4-7）用两个方程描述，即

和

将方程（4-8）和方程（4-9）称做幅值条件和相角条件，满足幅值条件和相角条件的s值，就是特征方程的根，即系统的闭环极点。当K*从零到无穷变化时，特征方程的根在复平面上变化的轨迹就是根轨迹。实际上，只要满足相角条件的点都是根轨迹上的点，当K*值确定之后，可依据幅值条件在根轨迹上确定相应的闭环极点。除了开环增益K（或根轨迹增益K*）外，系统其他参数变化时对闭环特征方程根的影响也可通过根轨迹表示出来，只要将特征方程整理后，使可变参数在K*的位置上，就可利用相角条件绘制出根轨迹来。