控制系统灵敏度分析解析

一个实际系统，无论其本质如何，都要受到环境条件改变、元件磨损老化和过程特性参数变化的影响。这些影响有时是很严重的，尤其是要求较高的场合。

控制系统在参数变化时的灵敏度是一个非常重要的概念。在开环系统中，所有的变化都会导致系统的输出产生偏差，并且系统自身没有能力消除这一偏差，这是由于开环系统没有反馈的缘故。但是，闭环系统能够察觉到输出所产生的偏差，并试图修正输出，这正是闭环反馈控制系统的一个主要好处，就是具有减少系统灵敏度的能力。

对于闭环系统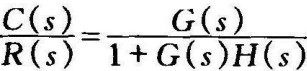的情况，如果在所关心的复数域内，都有

成立，则可得到

那么，输出仅受到H（s）的影响，而且H（s）有可能是一个常数。如果H（s）＝1，得到的结果正是期望的输入值，那就是，输出等于输入。但是，在对闭环控制系统应用式（3-72）这样一个近似之前，必须注意式（3-71）这一前提条件，可能会导致系统的响应为剧烈振荡，甚至于不稳定。尽管如此，增加开环传递函数G（s）H（s）的大小会导致G（s）对输出影响减少的事实是一个极有用的概念。因此，反馈控制系统的最重要优势就是被控过程参数G（s）变化的影响被减少了。

为描述参数变化的影响，假设被控过程G（s）发生变化，新被控过程就是G（s）＋△G（s）。那么，在开环情况下，输出的变化为

△C（s）＝△G（s）R（s）（3-73）

在闭环系统中，有

考虑到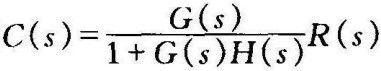，则输出的改变就是

通常情况下，有G（s）H（s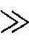）△G（s）H（s），于是

观察式（3-76）可以看出，由于[1＋G（s）H（s）]在所关心的复数域范围内常常远大于1，因此闭环系统输出的变化减少了。因子[1＋G（s）H（s）]在反馈控制系统的特征中起到了非常重要的作用。

系统灵敏度定义为系统传递函数的变化率与被控过程传递函数变化率的比值。如果系统传递函数为

GB（s）＝C（s）/R（s）

则灵敏度定义为

取微小增量的极限形式，则式（3-77）成为

很明显，从式（3-73）可以看出，开环系统的灵敏度等于1。闭环系统灵敏度可以从式（3-78）容易得到。设闭环系统的系统传递函数为

因此反馈系统关于G（s）的灵敏度为

即

再次可以看到，在所关心的复数域范围内G（s）H（s）增加时，闭环系统的灵敏度将会低于开环系统的灵敏度。(www.xing528.com)

同样道理，可以考察闭环系统对反馈环节H（s）改变时的系统灵敏度，令

即

当G（s）H（s）很大时，灵敏度约为1，也就是H（s）的变化将直接影响到系统的输出。因此，使用不随环境改变或基本恒定的反馈器件是很重要的。

由此可见，控制系统引入反馈环节后能减少因参数变化而造成的影响，尤其是因被控过程参数变化所造成的影响，这是反馈控制系统的一个重要优点。反馈系统的这种优点，在通讯工业中电子放大器的使用上得到了充分的体现。下面介绍一个利用反馈减少灵敏度的简单例子。

运算放大器是一种被广泛使用在电子线路上的集成电路器件，它的基本应用电路是图3-36（a）所示的反相放大器电路。通常，运算放大器的增益A远大于104。由于输入阻抗很高，所以运算放大器的输入电流可以忽略不计，因此在节点n，可写出电流关系式如下

由于放大器的增益是A，并且是反相接法，所以uc＝﹣Aun，因此

将式（3-83）代入式（3-82），得到

解出输出电压uc，有

可重写式（3-85）如下

当A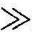1时，可忽略R1/Rf项，则

图3-36 反相放大器

其中，k＝R1/Rf。反相放大器电路结构图如图3-36（b），图中反馈环节是H（s）＝k，前向通道的传递函数是G（s）＝﹣A。进一步，当A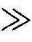1时，反相放大器电路的传递函数为

当运算放大器处于开环状态（即无反馈电阻Rf）时，相对于增益A的开环灵敏度为1。在闭环时，相对于增益A的闭环灵敏度为

如果A＝104，而且k＝0.1，有

则灵敏度接近于0.001，是开环灵敏度的千分之一。

再来考虑闭环时相对于因子k（或者反馈电阻Rf）的灵敏度。处理方法同上，得

相对于k的闭环灵敏度接近于1。