赫尔维茨判据详解

若系统特征方程式为

ansn＋an－1sn－1＋⋯＋a1s＋a0＝0

赫尔维茨判据为：系统稳定的必要和充分条件是an＞0的情况下，对角线上所有子行列式（如表中横竖线所隔）i（i＝1，2，⋯，n）均大于零。

赫尔维茨行列式由特征方程的系数按下述规则构成：主对角线上为特征方程式自an－1至a0的系数，每行以主对角线上的系数为准，若向左，系数的注脚号码依次上升；若向右，系数的注脚号码则依次下降；注脚号码若大于n或小于零时，此系数为零。

当n较大时，应用赫尔维茨判据比较麻烦，故它常应用于n较小的场合。事实上，赫尔维茨判据可由劳斯判据推导得到。

①当n＝1，特征方程式为

a1s＋a0＝0

稳定条件为a1＞0，△1＝a0＞0，即要求系统特征方程的所有系数为正数。

②当n＝2，特征方程式为

a2s2＋a1s＋a0＝0

稳定条件为 a2＞0，△1＝a1＞0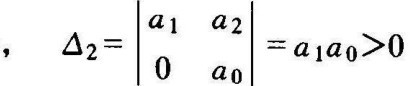

即只要特征方程的所有系数为正数，系统总是稳定的。

③当n＝3，特征方程式为(www.xing528.com)

a3s3＋a2s2＋a1s＋a0＝0

稳定条件为

即要求所有系数为正数，而且还需△2＞0。

④当n＝4，特征方程式为

a4s4＋a3s3＋a2s2＋a1s＋a0＝0

稳定条件为

所以，稳定条件是特征方程式所有系数为正数，还要△3＞0。

例3-10 设系统特征方程式为

s3＋7s2＋14s＋8＝0

试用赫尔维茨判据判别系统的稳定性。

解 从特征方程式看出所有系数为正数，满足稳定的必要条件。下面计算赫尔维茨行列式

所以系统是稳定的。