稳态误差计算方法详解

若控制系统的开环传递函数为

说明系统有N个积分环节串联。因为系统的类型常按其开环传递函数中串联积分环节的数目分类，所以称此系统为N型系统，当N＝0，1，2，⋯时，则分别称之为0型，1型，2型，⋯N型系统。增加型号数，可使系统精度提高，但对稳定性不利，实际系统中N≤2。GK（s）的其他零极点，对分类没有影响。

（1）单位阶跃输入时的稳态误差

设系统输入为单位阶跃信号，按式（3-47），系统的稳态误差为

令

Kp定义为位置误差系数，它实际上等于系统的开环放大系数。因此

对于0型系统，N＝0，则

对于1型或1型以上的系统，N≥1，则

由上述分析可知，由于0型系统中没有积分环节，对阶跃输入的稳态误差为一定值，其值基本上与系统开环放大系数K成反比，K愈大，ess愈小，但总有误差，除非K为无穷大。所以这种没有积分环节的0型系统，又常称为有差系统。

对于实际系统，通常允许存在稳态误差，只要它不超过规定指标就可以。所以有时为了降低稳态误差，常在稳态条件允许的前提下，增大Kp或K。若要求系统对阶跃输入的稳态误差为零，则系统必须是1型或1型以上的，即前向通道中必须具有积分环节。

（2）单位斜坡输入时的稳态误差

当参考输入为单位斜坡信号时，系统的稳态误差为

令

Kv定义为速度误差系数，所以

对于0型系统，N＝0，则

对于1型系统，N＝1，则

对于2型或高于2型系统，N≥2，则

以上表明，0型系统对于等速度输入（斜坡输入）不能紧跟，最后稳态误差为∞。具有单位反馈的1型系统，其输出能跟踪等速度输入，但总有一定误差，为使稳态误差不超过系统的规定值，K值必须足够大。对于2型或高于2型系统，稳态误差为零，这种系统有时称为二阶无差系统。

所以对于等速度输入信号，要使系统稳态误差为零，必须使N≥2，即必须有足够的积分环节数。(www.xing528.com)

（3）单位抛物线信号（等加速度信号）输入时的稳态误差

已知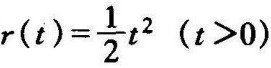，所以稳态误差

令

Ka定义为加速度误差系数，所以

对于0型或1型系统，N＝0或N＝1，则

对于2型系统，N＝2，则

对于3型或3型以上系统，N≥3，则

Ka＝∞，ess＝0

所以当输入为单位抛物线信号时，0型或1型系统都不能满足要求，2型系统能工作，但要有足够大的Ka或K。只有3型或3型以上的系统，当它为单位反馈时，系统输出才能紧跟输入，且稳态误差为零。但是必须指出，当前向通道积分环节数增多时，会降低系统的稳定性。

当输入信号是上述典型信号的组合时，为使系统满足稳态响应的要求，N值应按最复杂的输入信号来选定（例如输入信号包含有阶跃和等速度信号时，N值必须大于或等于1）。

综上所述，表3-3概括了不同类型系统在不同的输入信号作用下的稳态误差。

表3-3 系统的稳态误差ess

例3-2 已知两个系统如图3-26所示，当参考输入r（t）＝4＋6t＋3t2时，试分别求出两个系统的稳态误差。

图3-26 例3-2的系统

解 系统（a）为1型系统，其Ka＝0，不能紧跟r（t）中的3t2分量，所以

ess＝∞

系统（b）为2型系统，其Ka＝K＝10/4，所以

该例说明，当输入为阶跃、斜坡和抛物线信号的组合时，抛物线信号分量要求系统型号最高。系统（b）的型号为2，能跟随输入信号中的抛物线信号分量，但仍有稳态误差。而系统（a），由于型号较低，故不能跟随抛物线信号分量，稳态误差为∞。