控制系统传递函数简介

控制系统在工作过程中会受到两类外作用信号的影响。一类是有用信号，或称为输入信号、给定值、参考输入等，常用r（t）表示；另一类则是扰动，或称为干扰，常用n（t）表示。输入r（t）通常是加在系统的输入端，而干扰n（t）一般是作用在被控对象上，但也可能出现在其他元部件上，甚至夹杂在输入信号之中。一个闭环控制系统的典型结构可用图2-56表示。

图2-56 闭环控制系统典型结构

研究系统输出量c（t）的运动规律，只考虑输入量r（t）的作用是不完全的，往往还需要考虑干扰n（t）的影响。

基于后面章节的需要，下面介绍几个系统传递函数的概念。

（1）系统的开环传递函数

在图2-56中，将H（s）的输出通路断开，亦即断开系统的主反馈通路，这时前向通路传递函数与反馈通路传递函数的乘积G1（s）G2（s）H（s），称为该系统的开环传递函数。它等于此时B（s）与R（s）的比值。开环传递函数并不是第一章所述的开环系统的传递函数，而是指闭环系统在开环时的传递函数。

图2-57 r（t）作用下的系统结构图

（2）r（t）作用下系统的闭环传递函数

令n（t）＝0，这时图2-56简化为图2-57，输出c（t）对输入r（t）之间的传递函数

称GB（s）为在输入信号r（t）作用下系统的闭环传递函数。而输出的拉氏变换式

可见，当系统中只有r（t）信号作用时，系统的输出完全取决于c（t）对r（t）的闭环传递函数及r（t）的形式。

（3）n（t）作用下系统的闭环传递函数

图2-58 n（t）作用下系统的结构图

为研究干扰对系统的影响，需要求出c（t）对n（t）之间的传递函数。这时，令r（t）＝0，则图2-56简化为图2-58。由图可得

称Gn（s）为在干扰n（t）作用下系统的闭环传递函数。而输出的拉氏变换式

由于干扰n（t）在系统中的作用位置与输入信号r（t）的作用点不一定是同一个地方，故两个闭环传递函数一般是不相同的。这也表明引入干扰作用下系统闭环传递函数的必要性。

（4）系统的总输出

根据线性系统的叠加原理，系统的总输出应为各外作用引起的输出的总和。因而将式（2-88）与式（2-90）相加即得总输出量的变换式

例2-11 根据图2-28位置随动系统的结构图，试求系统在给定值θr（t）作用下的传递函数及在负载力矩ML作用下的传递函数，并求两信号同时作用下，系统总输出θc（t）的拉氏变换式。

解 ①θr（t）作用下系统的闭环传递函数θc（s）/θr（s）。令ML＝0，系统结构图简化为图2-59。运用串联及反馈法则（或梅逊公式），可求得

图2-59 ML＝0时系统结构图

②ML作用下系统的闭环传递函数θc（s）/ML（s）。令θr＝0，系统结构图如图2-60所示。经结构变换可求得

③系统总输出

在θr及ML同时作用下，系统的总输出为两部分叠加，即(www.xing528.com)

θc（s）＝Gθ（s）θr（s）＋Gm（s）ML（s）

（5）闭环系统的误差传递函数

在系统分析时，除了要了解输出量的变化规律之外，还经常关心控制过程中误差的变化规律。因为控制误差的大小，直接反映了系统工作的精度。故寻求误差和系统的控制信号r（t）及干扰作用n（t）之间的数学模型，就是很必需的了。在图2-56中，规定代表被控量c（t）的测量装置的输出b（t）和给定输入r（t）之差为系统的误差e（t），即

e（t）＝r（t）－b（t）或E（s）＝R（s）－B（s）

E（s）即图中综合点的输出量的拉氏变换式。

图2-60 θr＝0时系统结构图

①r（t）作用下的误差传递函数，取n（t）＝0时的E（s）/R（s）。则可通过图2-61求得

图2-61 r（t）作用下误差输出的结构图

②n（t）作用下系统的误差传递函数，取r（t）＝0时的E（s）/N（s）。通过图2-62可得

③系统的总误差，根据叠加原理可得

E（s）＝Ge（s）R（s）＋Gen（s）N（s）

图2-62 n（t）作用下误差输出的结构图

（6）闭环系统的特征方程

将上面导出的四个传递函数表达式（2-87）、式（2-89）、式（2-92）及式（2-93）相对比，可以看出它们虽然各不相同，但分母却是一样的，均为[1＋G1（s）G2（s）H（s）]，这是闭环控制系统各种传递函数的规律性。令

D（s）＝1＋G1（s）G2（s）H（s）＝0（2-94）

称为闭环系统的特征方程。如果将式（2-94）改写成如下形式

sn＋αn－1sn－1＋⋯＋α1s＋α0＝（s＋p1）（s＋p2）⋯（s＋pn）＝0（2-95）

则﹣p1，﹣p2，⋯，﹣pn称为特征方程的根，或称为闭环系统的极点。特征方程的根是一个非常重要的参数，因为它与控制系统的瞬态响应和系统的稳定性密切相关。

另外，如果系统中控制装置的参数设置，能满足∣G1（s）G2（s）H（s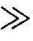）∣1及∣G1（s） H（s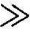）∣1，则系统的总输出表达式（2-91）可近似为

即

R（s）－H（s）C（s）＝R（s）－B（s）＝E（s）≈0

这表明，采用反馈控制的系统，适当地匹配元部件的结构参数，有可能获得较高的工作精度和很强的抑制干扰的能力，同时又具备理想的复现、跟随指令输入的性能，这是反馈控制优于开环控制之处。