典型环节及其传递函数分析

控制系统是由若干元件有机组合而成的。从结构上及作用原理上来看，有各种各样不同的元件，但从动态性能或数学模型来看，却可分成为数不多的基本环节，也就是典型环节。不管元件是机械式、电气式或液压式等等，只要它们的数学模型一样，它们就是同一种环节。这样划分，为系统的分析和研究带来很多方便，对理解和掌握各种元件对系统动态性能的影响也很有帮助。

以下列举几种典型环节及其传递函数。这些环节是构成系统的基本环节，有时简单的系统也可以用它们来描述，它们的阶数最高不超过2。

（1）比例环节

比例环节的传递函数为

G（s）＝K（2-71）

这表明，输出量与输入量成正比，不失真也不延滞，所以比例环节又称为无惯性环节或放大环节。无弹性变形的杠杆、不计非线性和惯性的电子放大器、测速发电机（输出为电压、输入为转速时）等都可认为是比例环节。

图2-18 比例环节

图2-18（a）所示为一电位器，它的输入电压经分压后作为输出电压，所以在不考虑负载效应时，电位器可以看成比例环节。这一环节的输入量和输出量关系，可用图2-18（b）所示的结构图来表示。

（2）惯性环节

凡传递函数具有如下形式的环节为惯性环节

式中 K——环节的比例系数；

T——环节的时间常数。

当环节的输入量为单位阶跃函数时，环节的输出量将按指数曲线上升，具有惯性，如图2-19（a）所示。RC回路、RL回路、直流电动机电枢回路（当电枢电感可忽略不计时）都可看做惯性环节。

图2-19 惯性环节

（3）积分环节

它的传递函数为

当积分环节的输入信号为单位阶跃函数时，则输出为t/T，它随着时间直线增长，如图2-20（a）所示。直线的增长速度由1/T决定，即T越小，上升越快。T称为积分时间常数。当输入突然除去，积分停止，输出维持不变，故有记忆功能。对于理想的积分环节，只要有输入信号存在，不管多大，输出总要不断上升，直至无限（当然，对于实际元件，由于能量有限、饱和限制等，是不可能到达无限的）。

图2-20 积分环节

实际上，比较图2-19（a）和图2-20（a）知道，当惯性环节的时间常数很大，在起始以后很长一段时间内，输出响应曲线近似为直线，所以这时惯性环节的作用就近似一个积分环节。

图2-20（b）为控制系统中经常应用的积分控制器。积分时间常数为RC。

（4）微分环节

理想微分环节的传递函数为

G（s）＝Ts（2-74）(www.xing528.com)

理想微分环节的输出量与输入量的一阶导数成正比。假如输入是单位阶跃函数1（t），则理想微分环节的输出为c（t）＝Tδ（t），是个脉冲函数。由于微分环节能预示输入信号的变化趋势，所以常用来改善控制系统的动态性能。

理想微分环节的实例示于图2-21（a）、（b）。其中（a）为测速发电机，当其输入为转角θ，输出为电枢电压时，则有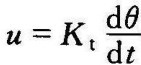。图中（b）为微分运算放大器，它是近似的理想微分环节（实际上，运算放大器作微分运算时，常接成隐式电路）。

在实际系统中，微分环节常带有惯性，它的传递函数为

图2-21 微分环节

它由理想微分环节和惯性环节组成，如图2-21（c）、（d）所示。只有在低频时，它们才近似为理想微分环节，否则就有式（2-75）的传递函数。

（5）振荡环节

该环节包含有两个储能元件，在输入信号作用时，两个储能元件进行能量交换。图2-22所示为单位阶跃函数作用下的响应曲线。它的传递函数为

式中 ωn—无阻尼自然振荡频率，ωn＝1/T；

ζ——阻尼比，0＜ζ＜1。

振荡环节实际上是一个二阶系统，对它的详细分析，将在第3章中进行。本章第2节中的机械位移系统、RLC电路、只考虑电枢电压控制作用的直流电动机（输出为转速）等，从传递函数的特性讲都是振荡环节。

图2-22 振荡环节的单位阶跃响应曲线

（6）延滞环节

在实际系统经常会遇到这样一种典型环节，当输入信号加入后，它的输出端要隔一定的时间后才能复现输入信号。例如图2-23所示，当输入为阶跃信号，输出要隔一定时间τ后才出现阶跃信号，在0＜t＜τ内，输出为零。这种环节叫做延滞环节，τ叫做延滞时间（又称死时）。延滞环节也是线性环节，具有延滞环节的系统叫做延滞系统。

图2-23 延滞环节

延滞环节的传递函数可求之如下

c（t）＝r（t－τ）

其拉氏变换为

式中ξ＝t－τ，所以延滞环节的传递函数为

G（s）＝e﹣τs（2-77）

系统中具有延滞环节，对系统的稳定性不利，延滞越大，影响越大。

大多数过程控制系统中，都具有延滞环节，例如燃料或其他物质的传输，从输入口至输出口有传输时间（即延滞时间），介质压力或热量在管道中的传播有传播延滞，以及各种机构运行中有延滞等。

以上是线性定常系统中，按数学模型区分的几个最基本的环节。一个元件可能是一个典型环节，也可能由几个典型环节组成。