非线性方程的线性化方法详解

严格地说来，几乎所有元件或系统的运动方程都是非线性方程。也就是说，输入、输出、扰动这些变量间的关系都是非线性的。但是对于许多元件或系统来说，以及对更多的元件或系统在比较小的范围运动来说，如果把这些关系看做是线性关系，是不会产生很大误差的。而且方程式一经线性化，由于可以应用叠加原理等原因，就使得研究问题时非常方便。所以常常利用线性化方法来简化所研究的系统。

例如，对于某些非线性系统，若研究的是系统在某一工作点（平衡点）附近的性能，或者说，研究的是系统变量在动态过程中偏离平衡点不大时的性能（如图2-10所示）， x0为平衡点，受到扰动后，x（t）偏离x0，产生△x（t） （△x（t）的变化过程，表征系统在x0附近的性能），则可以应用下述的线性化方法得到的线性模型代替非线性模型来描述系统，而实际系统就可按线性系统对待。这就是常说的“小偏差理论或小信号理论”。应用线性化数学模型代替原来的非线性模型，这一过程就是线性化过程。

图2-10 小偏差过程

例如上节介绍的磁场控制的直流电动机。假定电枢电压ua为常值，输出为ω，控制输入为uf。如果考虑i与φ之间的非线性关系，其数学模型是相当复杂的非线性微分方程。假如现在研究的是它的小偏差过程，例如控制输入uf改变一个微量△uf引起的变化过程。那么描述这个过程的偏量微分方程式，经过适当处理，将是线性方程式，这对分析研究提供了很大的方便。以下就看如何求出电动机输出输入偏量的微分方程式。

（1）根据物理或化学定律列出原始方程式

为此对激磁电路有

（2）找出中间变量φ与其他变量的关系，同时线性化

前已述及φ是if的非线性函数，所以式（2-38）是非线性方程式。由于是讨论小偏差过程，可用以下办法使之线性化。

设在平衡点的邻域内，φ对if的各阶导数（直至n＋1）是存在的，它可展成泰勒级数

式中Rn＋1为余项，φ0和if0为原平衡点的磁链和激磁电流，，⋯为原平衡点处的一阶、二阶、⋯导数，

△if＝if－if0（2-40）

图2-11 的求取

为激磁电流的偏量。

由于△uf很小，因此△if也很小，微量的高次项就更小，故式（2-39）右端第三项及其以后的各项均可忽略不计，式（2-39）变为

其中可由图2-11所示的工作曲线求得

称为动态电感，它为常值，但在不同平衡点，它有不同的值。因此式（2-41）可写为

或

上式说明在平衡点附近，经过线性化处理（忽略偏量的高次项）后，激磁回路偏量间具有线性关系了。偏差愈小，这个关系愈准确。

（3）求以偏量表示的微分方程式，即线性化方程式

将uf＝uf0＋△uf，，if＝if0＋△if代入式（2-38），则得

在平衡点，式（2-38）成为

式（2-44）与式（2-45）相减，就得激磁回路偏量微分方程式

它是关于偏量的线性方程式，只是的值随工作点不同而不同。式（2-46）通常可直接对式（2-38）两边取增量求得，从而简化推导过程。

若令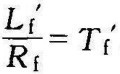，它为激磁回路动态时间常数（s），则有

式（2-47）表明，由于考虑各变量的偏量为微量，就把原来非线性数学模型，转化成以偏量表示的常系数线性数学模型了。在线性化过程中，由于只考虑泰勒级数中的一次偏量，故式（2-47）又称为一次线性化方程式。当然，在有些场合，非线性并不严重，偏量可以很大，这时线性化模型愈接近线性模型，甚至只是变量形式不同而已（即后者以偏量为变量）。

要建立整个系统的线性化微分方程式，首先要确定系统处于平衡状态时，各元件的工作点；然后列出各元件在工作点附近的偏量方程式，消去中间变量；最后得到整个系统以偏量表示的线性化方程式。假如有些元件方程式本来就是线性方程，为了使变量统一，可对线性方程式两端直接取偏量，即得以偏量表示的方程式。

下面举一个反馈控制系统的例子，来进一步说明系统的线性化方程式如何建立。

例2-1 图2-12表示直流电动机转速自动镇定系统，电动机的转速由输入电压ur给定。给定后，ur值保持不变，希望电动机转速不受任何扰动影响，保持给定的值（允许有一定误差，但稳态误差不能超过规定值）。稳态时，放大器输入e≠0，uf有一定值，保证电动机有必要的激磁电流if。任何扰动都将引起转速的变化，系统通过测速发电机反馈自动调节if，使转速保持基本不变。现在设电枢电压ua恒定，转速变化由负载转矩变化引起。求输入为负载转矩、输出为转速的系统的偏量微分方程式。

图2-12 直流电动机转速自动镇定系统(www.xing528.com)

图2-13 信号以偏量表示的系统结构图

解 ①稳态时，系统平衡，各信号稳态值为ω0，ut0，e0，uf0，if0，ia0等，负载转矩为ML0。现在负载转矩发生变化，但变化不大，为△ML，故各处信号（变量）均在稳态值附近不大范围内变动，其系统结构图见图2-13。它们的偏量方程式可求之如下。

a.激磁回路，由式（2-47）决定。

b.电枢回路

式中ea为电枢反电势，是中间变量，它由Φω决定，即

在此，是常数，上式是非线性方程式。

式（2-49）代入式（2-48），取增量后，得电枢回路线性化方程式为

或

式中Ta＝La/Ra为电枢回路时间常数，s。

c.电动机

故

式中为常数。上式仍为非线性方程式，要进行线性化。由于△ML0，则线性化后

式（2-50）和式（2-52）中△Φ是中间变量，它与△if有关系。气隙磁通Φ是if的非线性函数，它可由电动机空载曲线求得。由于是小偏差过程，和激磁回路一样，对它进行线性化后，可得

△Φ＝Cf△if（2-53）

式中 Cf在某一平衡工作点是常数，不同工作点，它具有不同的值。

联解式（2-47）、式（2-50）、式（2-52）和式（2-53）后，电动机线性化方程式为

式中后者为电动机的传递系数，在一定的工作点附近，它们都是常数。

d.放大器 认为没有惯性，而且是线性的，则直接可得

△uf＝Ka△e（2-55）

假如特性为非线性的，则上式为线性化方程式。

e.测速发电机

△ut＝Kt△ω（2-56）

f.比较器 因为△ur＝0，故

△e＝﹣△ut（2-57）

②从式（2-54）～式（2-57）消去中间变量△uf，△e和△ut后，即得到该系统在扰动输入△ML作用下的线性化微分方程式

式中K＝KmfKaKt为系统开环放大系数。

一般为了书写方便，常省略方程式中偏量的符号“△”，例如△ω，d△ω/dt写作ω， dω/dt，但在系统具有非线性场合，线性方程式中的变量均应理解为偏量。这样式（2-58）就可写作