微分方程式的建立方法及应用初探

下面举几个例子说明。

（1）弹簧-质量-阻尼器系统

在控制系统中，经常会碰到机械运动部件，它们的运动通常分为平移和旋转。列写机械运动部件的微分方程式时，直接或间接应用的是牛顿定律。

图2-1表示一个弹簧-质量-阻尼器系统。当外力f（t）作用时，系统产生位移y（t），要求写出系统在外力f（t）作用下的运动方程式。在此，f（t）是系统的输入，y（t）是系统的输出。列出的步骤如下。

图2-1 弹簧-质量阻尼器系统

①设运动部件质量用M表示，按集中参数处理。

②列出原始方程式。根据牛顿第二定律，有

式中 f1（t）——阻尼器阻力；

f2（t）——弹簧力。

③f1（t）和f2（t）为中间变量，找出它们与其他因素的关系。由于阻尼器是一种产生粘性摩擦或阻尼的装置，活塞杆和缸体发生相对运动时，其阻力与运动方向相反，与运动速度成正比，故有

式中 B为阻尼系数。

设弹簧为线性弹簧，则有

f2（t）＝Ky（t）（2-3）

式中K为弹性系数。

④将式（2-2）和式（2-3）代入式（2-1），经整理后就得这一系统的微分方程式

式中，M，B，K均为常数，故上式为线性定常二阶微分方程式，则此机械位移系统为线性定常系统。

式（2-4）还可写成

令

则有

计算时若采用国际单位制，即[f（t）]为N，[t]为s，[M]为kg，[y（t）]为m，[B]为N·s/m，[K]为N/m，则

所以TB和TM是图2-1所示系统的时间常数。称1/K为该系统的传递系数，它的意义是：在静止时，系统的输出与输入之比（系统静止时，它的输出不随t变化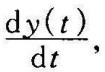 均为零）。

一般列写微分方程式时，输出量及其各阶导数项列写在方程式左端，输入项列写在右端。由于一般物理系统均有质量、惯性或储能元件，左端的导数阶次总比右端的高。在本例中，有质量M，又有吸收能量的阻尼器B，系统有两个时间常数，故左端导数项最高阶次为2。

（2）RLC电路

设在图2-2所示RLC电路中，R，L，C均为常值， ur（t）为输入电压，uc（t）为输出电压，输出端开路（或负载阻抗很大，可以忽略）。要求列出uc（t）与ur（t）的关系方程式。

图2-2 RLC电路

①根据克希霍夫定律可写出原始方程式

②式中i是中间变量，它与输出uc（t）有如下关系

③消去式（2-5）、式（2-6）的中间变量i后，便得输入输出微分方程式

或

式中T1＝L/R，T2＝RC为该电路的两个时间常数。当t的单位为s时，它们的单位也为s。图2-2电路的传递系数为1。

式（2-7）或式（2-8）也是线性定常系统二阶微分方程式，由于电路中有两个储能元件L和C，故式中左端导数项最高阶次为2。

比较式（2-4）和式（2-7）可知，当两个方程式的系数相同时，从动态性能角度来看，两个系统是相同的。这就有可能利用电气系统来模拟机械系统，进行试验研究。而且从系统理论来说，就有可能撇开系统的具体物理属性，进行普遍意义的研究。

（3）直流电动机

直流电动机经常应用在输出功率较大的控制系统中，它有独立的激磁磁场，改变激磁或电枢电压均可进行控制。

①电枢控制的直流电动机。

图2-3表示磁场固定不变（激磁电流If＝常数），用电枢电压来控制的直流电动机。设它的控制输入为电枢电压ua，它的输出轴角位移θ（用在位置随动系统时）或角速度ω （用在转速控制系统时）为输出，负载转矩ML变化为主要扰动。现欲求输入与输出关系微分方程式。

图2-3 电枢电压控制的直流电动机

a.考虑一般电机补偿是良好的，在反应速度不是很快的场合，可以不计电枢反应、涡流效应和磁滞影响；当If为常值时，磁场不变，并认为电机绕组温度在瞬变过程中是不变的。如此假设在工程上是允许的。

b.列写原始方程式。首先根据克希霍夫定律写出电枢回路方程式如下

式中 La——电枢回路总电感，H；

Ra——电枢回路总电阻，Ω；

Ke—电势系数，V/rad/s；

ω——电动机角速度，rad/s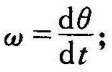

ua——电枢电压，V；

ia——电枢电流，A。

又根据刚体旋转定律，可写运动方程式

式中 J——转动部分转动惯量，kg.m2（折算到电动机轴上）；

ML——电动机轴上负载转矩，N·m；

Md——电动机转矩，N·m。

c.Md和ia是中间变量。由于电动机转矩与电枢电流和气隙磁通的乘积成正比，现在磁通恒定，所以有

Md＝Kmia（2-11）

式中 Km——电动机转矩系数，N·m/A。

d.将式（2-11）代入式（2-10），并与式（2-9）联立求解，整理后得

或

式中 Tm——机电时间常数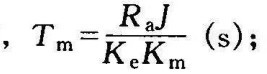

Ta——电动机电枢回路时间常数，一般要比Tm小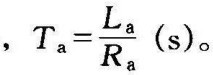

式（2-13）就是电枢电压控制的直流电动机微分方程式。其输入为电枢电压ua，输出为角速度ω，而负载转矩ML是另一种输入，即扰动输入。ML变化会使ω随之变化，它对电动机的正常工作产生影响。所以式（2-13）明确表达了电动机输出角速度与电枢电压和扰动之间的关系。

若输出为电动机的转角θ，则按式（2-13）有

式（2-14）是一个三阶线性定常微分方程。

②磁场控制的直流电动机。

图2-4所示系统主要用于恒定功率负载或电枢电流能保持恒定的场合，或者用在自动整定转速系统中。现设电枢电流Ia＝常数，气隙磁通Φ（t）＝Kfif（t），其中Kf为常数，即铁心不饱和，工作在线性段。建立输入输出关系方程式的步骤如下。

图2-4 磁场控制的直流电动机

a.假设铁心不饱和，则激磁回路电感Lf为常值。其他简化与电枢控制时相同。

b.激磁回路方程式

式中 uf——激磁电压，V；

if—激磁电流，A；

Rf——激磁回路电阻，Ω；

φ——激磁绕组磁链，Wb。

设电动机转矩Md是用来克服系统的惯性和负载的阻尼摩擦的，因此有(www.xing528.com)

式中 J——转动部分转动惯量；

B——阻尼摩擦系数。

c.中间变量有φ，Md。根据a.中简化和Ia＝常值的假设有

φ＝Lfif（2-17）

Md＝KmΦ＝KmKfif＝Kiif（2-18）

式中 Km，Kf为常数，Ki＝KmKf。

d.将式（2-17）和式（2-18）分别代入式（2-15）和式（2-16），消去中间变量，最后可得磁场控制的直流电动机的方程式

或

式中 Tf——激磁回路时间常数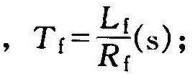

Tm——惯性和阻尼摩擦时间常数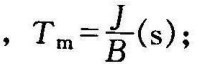

Kd——电动机传递系数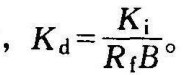

图2-5 激磁绕组的φ（if）曲线

由式（2-20）可知，磁场控制的直流电动机方程式，在假定条件下对ω仍为二阶线性方程式。实际上，φ是if的非线性函数（如图2-5所示），由式（2-15）、式（2-16）和式（2-18）得到的电动机方程式，将是很复杂的非线性方程式，求解就相当困难。

但若研究的是电动机在某一工作点附近的动态性能，应用上述的线性化方法得到的线性化方程式，就可充分准确地代替非线性方程式，因而也可以用线性理论来进行分析。

（4）电动机转速控制系统

图2-6是一个反馈控制系统。要建立反馈系统的方程式，应先画系统的结构图，明确各元件作用关系，如图2-7所示。然后写出各元件的微分方程式，消去中间变量，就可得到所求的输入输出关系方程式。对图2-6所示系统，其输出为角速度ω，参考输入为ur，扰动输入为负载转矩ML。系统的方程式具体列写如下。

①列各元件方程式。电动机方程式为式（2-13），即

图2-6 电动机转速控制系统

图2-7 系统的结构图

设放大器没有惯性，输出与输入成正比，即

ua＝Kae（2-22）

测速发电机输出为ut，输入为ω，故有

ut＝Ktω（2-23）

式中Kt为测速反馈系数。

e是参考输入ur和反馈电压ut之差，即

e＝ur－ut（2-24）

②消去中间变量。从式（2-13）、式（2-22）、式（2-23）和式（2-24）中消去中间变量ua，e， ut，最后得到系统的微分方程式

式中，为各元件传递系数的乘积，称为系统的开环放大系数。

若把所建立的系统微分方程式与式（2-13）比较，可以看出，假如K足够大，由于应用了反馈，扰动ML对转速的影响大大降低（为原来的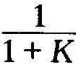），所以控制精，度提高了。

（5）热力系统

图2-8表示一个热水供应系统，为了保证一定的热水温度θ0，由电热器提供热流量φi（W）。在本系统中，输入量为φi，输出量为θ0。假定环境温度为θi，进水温度也是θi，并且水箱中各处温度相同（即用集中参数代替分布参数），这样简化后系统方程式可列写如下。

图2-8 热力系统

①按能量守恒定律可写出热流量平衡方程

φi＝φt＋φo－φc＋φs（2-26）

式中 φt—供给水箱中水的热流量，W；

φ0——出水带走的热流量，W；

φc——进水带入的热流量，W；

φs——通过热绝缘耗散的热流量，W。

②找出中间变量与其他因素关系

式中 C——水箱中水的热容量，J/℃；

θ0——水箱中水的温度，℃。

式中 Q——出水流量，kg/s；

cp—水的比热容，J/kg·℃。

式中 R——由水箱内壁通过热绝缘扩散到周围环境的等效热值，℃/W。

③将以上各式代入热平衡方程，便得系统的微分方程式

或

式中T＝RC为热时间常数，s。

这是一个一阶非线性微分方程式。影响热水温度θ0的扰动有出水流量Q和进水温度θi。当出水流量Q一定，环境温度和进水温度θi也为常值时，可令

θ＝θ0－θi（2-32）

θ为温升，系统输出为温升时的微分方程式为

式（2-33）为一阶线性定常微分方程。

图2-9 流体过程

（6）流体过程

图2-9中流入流量为Qi，流出流量Qo，它们受相应的阀门控制。设该系统的输入量为Qi，输出量为液面高度H，则它们之间的微分方程式可列写如下。

①设流体是不可压缩的，根据物质守恒定律，

可得

或

式中 S——液罐截面积，m2；

H——液面高度，m；

Qi，Qo—流入、流出流量，m3/s。

②求出中间变量Qo与其他变量的关系。由于通过节流阀的流体是紊流，按流量公式可得

式中 α为节流阀的流量系数（m2.5/s），当液体变化不大时，可近似认为只与节流阀的开度有关，现在设节流阀开度保持一定，则α为常数。

③消去中间变量Qo，就得输入输出关系式

它是一阶非线性微分方程式。

从上述两个例子得到的非线性方程说明，很多过程控制中控制对象具有非线性特性。

以上阐明了如何建立一个系统微分方程式的过程。对于任何线性定常系统，假如它的输出为c，输入为r，则系统方程式的一般形式如下

式中ai（i＝0，1，⋯，n），bi（i＝0，1，⋯，m）为常数，对于实际系统来说，n≥m，而大多数系统n＞m。