工程数据的处理方法优化技巧

技术资料如数据、表格、曲线等，必须预先将其存入计算机中，才能在设计时灵活方便地调用。为此，有必要学习掌握工程数据的处理方法及CAD程序编制方法。

对工程数据的处理有如下三种方式：

1）将工程数据转换为程序存入计算机内存。

2）将工程数据转换为数据文件存入计算机外存。

3）将工程数据转换为数据结构存入数据库。

以下分别介绍工程数据的处理方法。

1.数表的分类与存取

（1）数表的分类 一般按照数表中的数据之间有无函数关系，将其分为简单数表和列表函数表，或按数表的维数分为一维数表和二维数表。

1）列表函数表。该数表中所记载的一组数据，彼此之间存在着一定的函数关系。它又细分为两类：

①有计算公式的列表函数表。即当初是根据理论计算公式或经验公式建立的列表函数表。只是由于公式本身复杂，为便于手工计算，才将该公式以数表的形式给出。如齿轮的齿形系数表、轴的应力集中系数表、特定条件下单根V带所能传递的功率表等。故在编制CAD程序时，对此类数表可直接利用原来的公式进行有关数据的计算。

②无计算公式的列表函数表。是指通过实验观测并根据经验加以修正而得到的一些离散数据表。它是以表格函数的形式来表示参数间的函数关系。

对此类数表可利用程序设计语言的“数组”进行存储。但在检索时，尚需采用插值方法来检取数据。

2）简单数表。该表是指表中的数据彼此之间不存在函数关系的一些离散量。只是记载了一些不同对象之间的各个常数关系。如各种材料的力学性能、齿轮的标准模数系列、V带轮的计算直径系列、各种材料的密度表等。对此类数表也是利用程序设计语言的数组进行存储，但在检索时，不存在插值问题，因为它们之间无函数关系。

3）一维数表。该表是指其数据只与一个变量相关的数表。如表8-7所示的V带传动的包角系数K_α表。

表8-7 V带传动的包角系数K_α

4）二维数表。是指其数据同时与两个变量相关的数表。如表8-8所示的V带传动的长度系数K_L表。

表8-8 V带传动的长度系数K_L

（2）数表的存取 一般将数据按一定规则排列，然后存入数组。一维数表采用一维数组存储，二维数表用二维数组存储。而查取数据时，则需用逻辑判断语句通过比较得到所需数据。

2.线图的分类与处理

线图可直观地表现参数间的函数关系和变化趋势。但CAD程序不能直接查取线图，必须将其处理成为程序能够检索的形式。而处理的方法与线图的类型有关。线图根据其数据来源分为以下两类：

（1）有计算公式的线图 如图8-12所示的齿轮接触强度计算中的螺旋角参数Z_β曲线，实际上是根据计算公式Z_β=cosβ绘制的。因此，在CAD程序中，可直接使用该公式进行计算。

（2）无计算公式的线图 对于此类线图有如下两种处理方法：

1）数表化处理。即首先将线图转换成数表形式，然后按前述数表的方法进行处理。如图8-13所示为蜗轮齿形系数Y₂与齿数Z₂之函数关系。首先在线图上取一系列不同的齿数Z₂，并找出与其对应的齿形系数Y₂。然后将这些数对（Y₂，Z₂）列成一维数表，如表8-9所示。

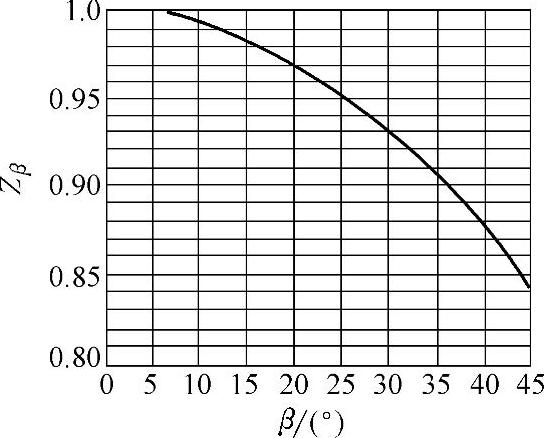
图8-12 齿轮接触强度计算中的螺旋角参数

图8-13 蜗轮齿形系数Y₂曲线

关于节点的选取原则是：应使各相邻结点间函数值的差值均匀，即在曲线陡峭处节点区间应取小些，而在曲线平滑处节点区间应取大些。

由于线图是反映参数间的函数关系，所以转换后的数表属于列表函数表。如当需要查取的数据不在节点上时，需要进行插值运算。

表8-9 蜗轮齿形系数Y₂（变位系数ζ=0，α=20°，h_a=1）

2）公式化处理。对于直线或折线图，可将其转化成线性方程，用以表示参数间的关系。并分为以下三种类型：

①直角坐标系直线图。如图8-14所示为直齿轮和斜齿轮的动载荷系数K_v曲线，共16条直线。若采用数表转换法则要占用很大内存，故宜采用公式处理。

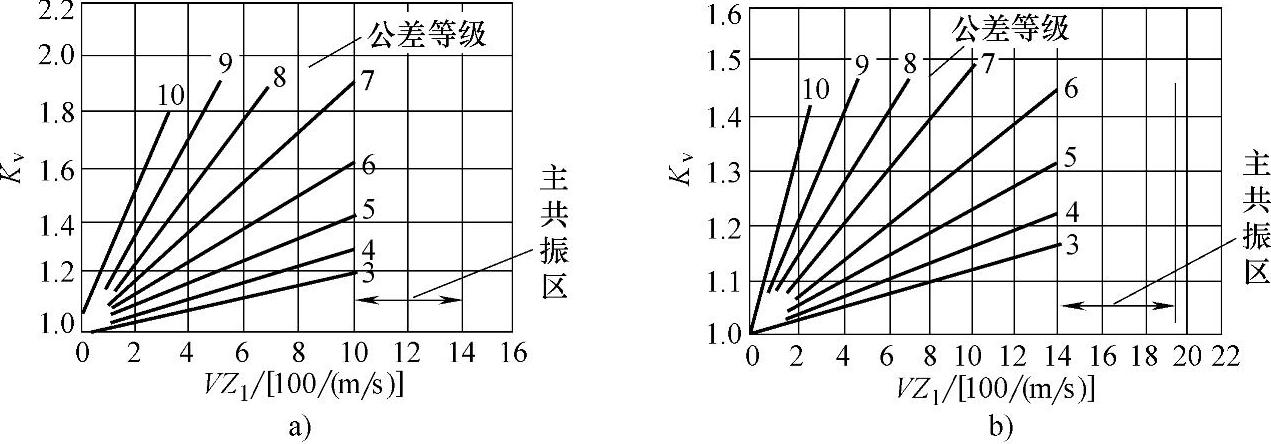
图8-14 直齿轮和斜齿轮的动载荷系数K_v曲线

在图中每条直线上任取两点，以其坐标（x₁、y₁）、（x₂、y₂）建立两点式直线方程如下：

利用该方程即可计算出任意VZ₁所对应的动载荷系数K_v。

②对数坐标系直线图。图8-15所示为各类钢材的弯曲强度寿命系数Y_N曲线。其转换方法如下：首先，在对数直线上任取两点（lgx₁，lgy₁）、（lgx₂，lgy₂），即可求出如下对数方程：

(www.xing528.com)

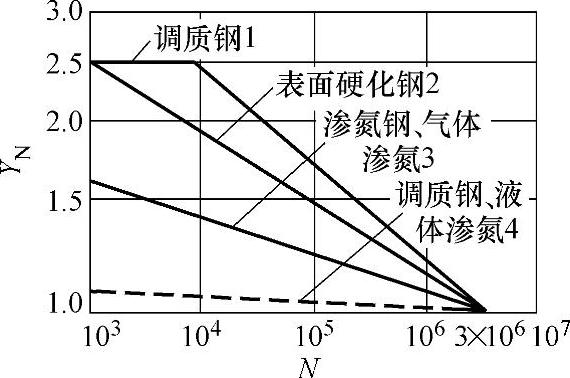
图8-15 各类钢材的弯曲强度寿命系数Y_N曲线

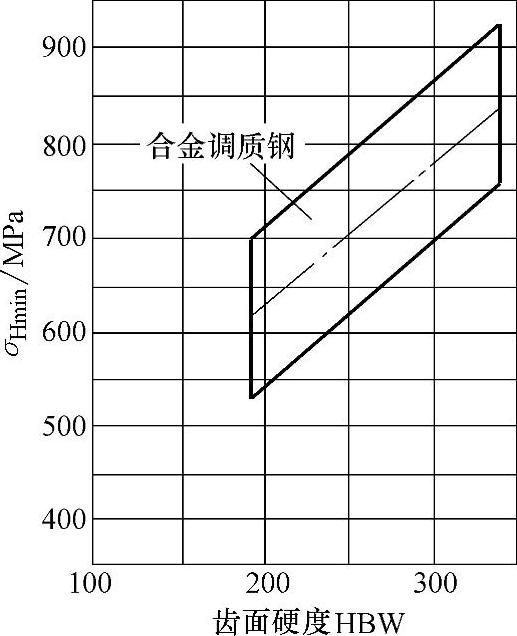
图8-16 齿轮材料接触疲劳强度极限应力σ_Hmin区域图

令：c=lgy，则：y=10^c（8-3）

利用式（8-2）和式（8-3）即可求出各种钢材任意应力循环次数N下所对应的寿命系数Y_N。

③由折线组成的区域图。如图8-16为齿轮材料接触疲劳强度极限应力σ_Hmin区域图（由于其影响因素很多，如材料成分、热处理方式、硬化层深度、构件尺寸等，因此采用区域图表示）。可采取按区域图中线取值的方法进行转换。即在中线上任取两点（HBW1，σ_H1）、（HBW2，σ_H2），然后求出其方程：

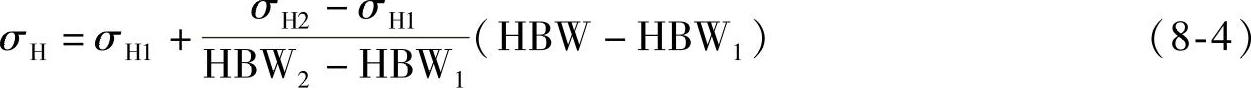
利用该公式即可求出任意齿面硬度HBW所对应的接触疲劳强度极限应力σ_Hmin。

3.列表函数表的插值算法

如表8-15带传动包角系数K_α，如给出的包角α不是表中所列节点值，如α=125°。此时要检索K_α就需要用插值算法计算。

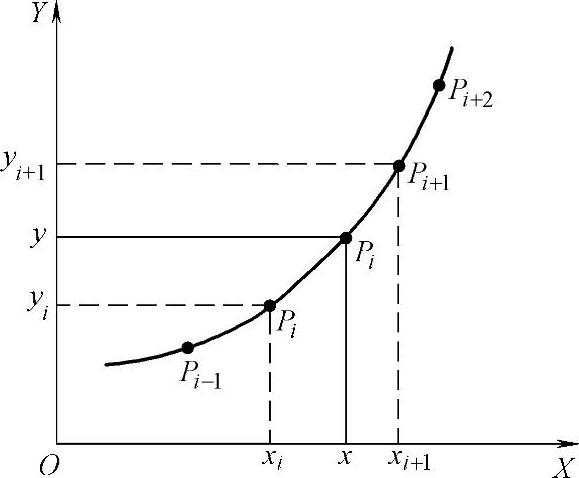
图8-17 线性插值算法示意图

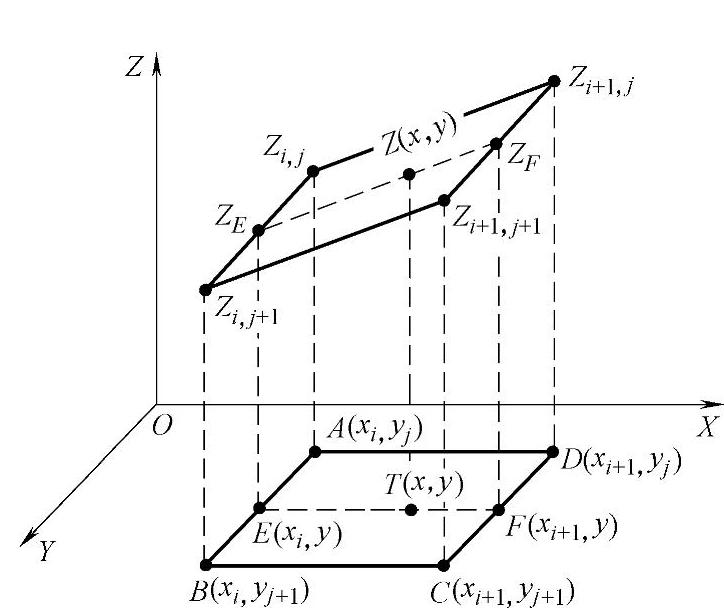
图8-18 二维列表函数表的线性插值算法

（1）一维列表函数表的插值 列表函数表的插值算法的基本思路是：在插值点附近选取几个合适的节点，利用它们构造一个简单的函数g（x），近似代替列表函数f（x）。

插值运算方法有线性插值算法和抛物线插值算法两种。常用线性插值算法及其标准程序如下：

1）线性插值算法，如图8-17所示。一维列表函数y=f（x）可用一元函数曲线表示。如欲求P（x，y）点之函数值y的线性插值算法如下：首先在曲线上找到与插值点P相邻的两个节点P_i和P_i+1，然后求出如下插值公式：

2）一维线性插值函数编成标准程序（略）。

（2）二维列表函数表的插值 二维列表函数的关系式为

z_i，j=f（x_i，y_i）（i=0，1，2，…，m；j=0，1，2，…，n）当需要用插值法在二维列表函数表中查取数据时，同样有线性插值算法和抛物线插值算法两种方法。现将比较常用的线性插值算法介绍如下

1）二维列表函数表的线性插值算法，见图8-18

①先从二维数表所给定M×N个节点中，选取最接近于插值点T（x，y）的相邻四个节点。

②然后分别调用三次一维线性插值算法，即可计算出与插值点T（x，y）相对应的函数值Z（x，y）。

③如图8-18所示，与插值点T（x，y）最接近的相邻四个节点分别为A、B、C、D；其函数值均已知。

④第一次由A、B两点，用一维线性插值算法计算出E（x_i，y）的插值函数值Z_E。

⑤再由C、D两点，用一维线性插值算法计算出F（x_i+1，y）的插值函数值Z_F。

⑥第三次由E、F两点，用同样方法计算出T（x，y）的插值函数值Z（x，y）。

由所示算法可得二维插值公式：

z（x，y）=（1-a）（1-b）z_i，j+b（1-a）z_i，j+1+a（1-b）z_i+1，j+abz_i+1，j+1（8-6）

式中 ，

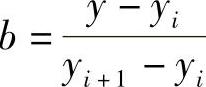
2）二维线性插值函数编成标准程序（略）。

4.数据的公式拟合

由于计算机处理公式比处理数据表要简单得多，所占内存小得多，因此要尽可能地将数据拟合为公式。数据的公式拟合方法是指将试验曲线或一系列实测数据的基础上，建立起相应的近似的经验公式的过程。其拟合步骤是：首先决定函数类型，然后决定函数的各项系数。而确定函数系数有两种方法：即多项式的最小二乘法拟合和指数曲线拟合。

5.数据文件及其应用

（1）采取数组形式存储图表方法的局限性 上述以数组形式将数表和线图存入计算机内存的方法有以下局限性：

1）需要过多地占用计算机内存。

2）无法实现数据共享。因为这些数表和线图数据只能与特定的CAD计算程序相连，而不能为其他程序共享。

（2）建立数据文件的优点 为了克服以上不足，宜将数表和线图单独建立用户数据文件，并按指定的文件名存放在计算机外存储器上，且使其独立于计算机程序。使得一个数据文件可供不同的计算机程序调用。因此，不仅解决了大量占用内存的问题，而且实现了数据的共享。