结构精度是指组成产品的零部件的形状、尺寸以及相对位置的准确程度。它直接关系着产品功能实现的质量。例如合理提高传动系统零件的精度,不仅有利于提高其运动规律的准确性和运动的平稳性、降低噪声、减轻振动;而且可以提高系统的承载能力。但是,加工精度的提高一般会提高成本。因此,正确的结构设计应该是在相同成本的前提下,力求获得较高的结构精度。这正是本节所探讨的主题。下面将针对不同类型误差产生的原因,提出有利于减少误差的各种结构设计方法。
(1)有利于减少原始误差的结构设计方法 在相同加工条件下,较小的公称尺寸和较小的测量范围,更容易实现较高的精度。因此,对有精度要求的结构要素,应在保证结构功能前提下,尽量减小其公称尺寸和精度约束的范围。如图6-108为两种轴系结构方案的对比。其中,与齿轮相配合的轴颈和与右侧轴承配合的轴颈尺寸精度和表面粗糙度要求较高;而与密封毡圈相配合的轴段的尺寸精度要求较低。如果按图a方案,将其分为不同直径的三个轴段,应该是合理的。而图b方案采取将三个轴段合并,不仅使得高精度轴段的长度增大,而且实现精度要求的难度也加大,故此方案不宜采用。
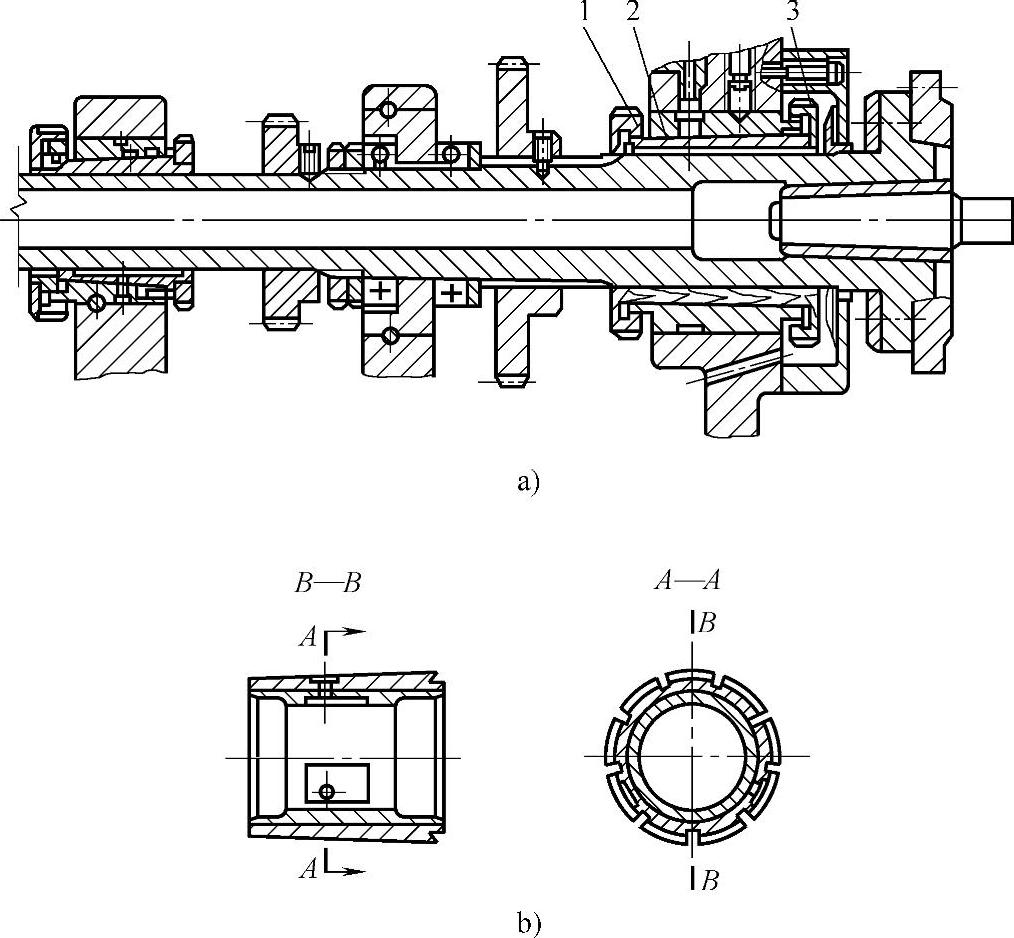
图6-107 车床主轴部件的可调节轴承
1、3—螺母 2—轴承
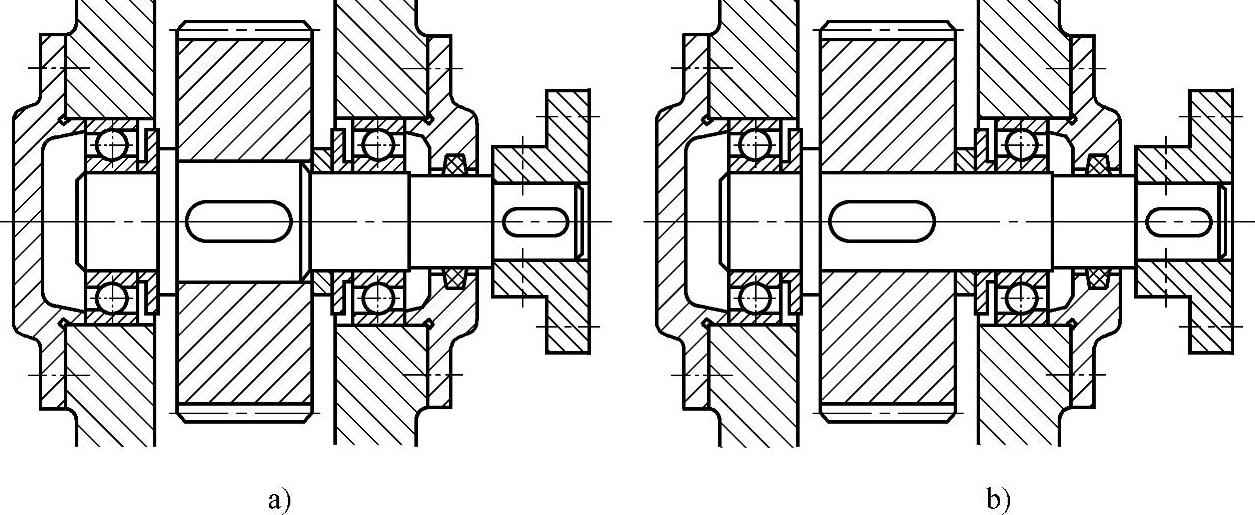
图6-108 两种轴系结构方案的对比
当某个作用尺寸由多个尺寸元素构成时,则该尺寸的公差等于各组成元素尺寸公差之和。因此,组成元素越多,作用尺寸的精度就越低。所以,对于要求精度较高的尺寸,应尽量减少其组成元素的数量,尽量使得作用尺寸可以直接得到。
如图6-109所示,为避免误差积累,图中给出了作用尺寸“120”的两种标注方法。其中,图b方案作用尺寸120由三个基本尺寸组成,故其积累误差大,尺寸精度低,不可取;而图c方案使得该作用尺寸可以直接得到,因而避免了误差积累,提高了尺寸精度。
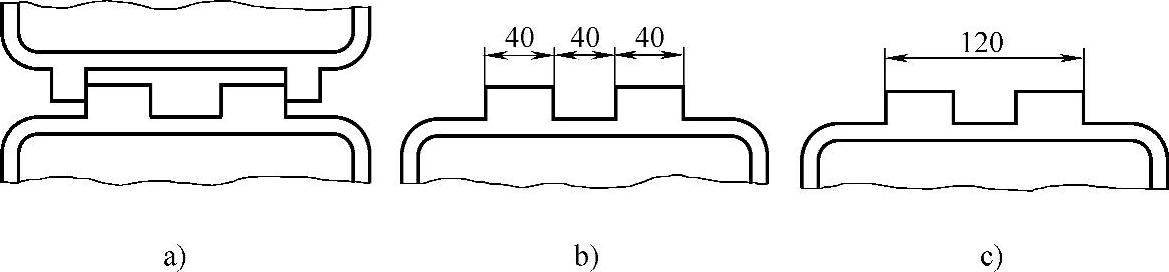
图6-109 避免误差积累
当作用尺寸由于结构限制,不可避免地由多个尺寸元素组成时,可以在组成元素中设置一个调整环节,通过尺寸调整来实现作用尺寸的精度要求。例如图6-108中,在轴承端盖与箱体之间的垫片,就是一个调整环节。由于轴承的轴向间隙可以调整,因而降低了构成轴承间隙的其他尺寸的精度要求。
(2)通过补偿系统误差来提高精度的方法 对于已知影响因素的系统误差,可根据引起误差的原因,分别采取校正、抵消和调整的方法进行补偿。
1)校正。例如通过螺纹校正装置来纠正由于基准丝杠螺距误差而引起的加工误差。丝杠螺距误差校正装置的原理详见图6-110。首先通过测量得到丝杠螺距误差曲线(即丝杠螺距误差随丝杠长度变化的规律),然后将此曲线按需要比例放大,得到校正曲线并制作凸轮校正板,在刀架移动过程中,校正板推动顶杆,顶杆再通过杠杆齿轮将运动传递给螺母,并使得螺母做微小的转动。正是由于螺母的这种微小的转动使得螺旋传动的从动件产生附加移动,因而补偿了由于丝杠螺距误差而造成的运动误差。
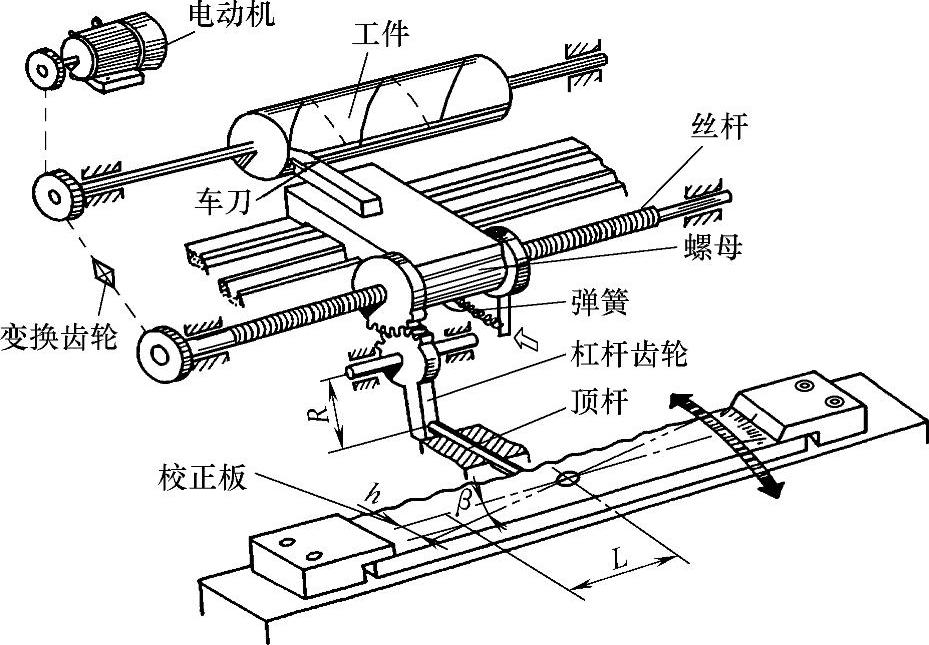
图6-110 丝杠螺距误差校正装置的原理
2)抵消。由于零件接触表面的磨损导致零件形状和尺寸的变化。抵消是指通过结构设计,使得多个相关零件的磨损对于某个执行零件的作用产生互相抵消,以达到提高执行零件的动作精度的目的。如图6-111所示为凸轮机构磨损量的抵消原理。图6-111a中,凸轮与摆杆之间的接触点及摆杆与执行零件之间的接触点的磨损量对于执行零件的工作位置的影响呈互相叠加关系。而对于图6-111b,该两点的磨损量对于执行零件的工作位置的影响呈互相抵消关系,因此,可以使得执行零件的动作精度得以提高。
3)调整。如果在既不能校正、又不能抵消的情况下,则可以在结构中设置调整环节。当磨损量积累到一定程度后,再通过调整来恢复系统的正常工作状态。如图6-112所示的轴承的间隙调整结构。
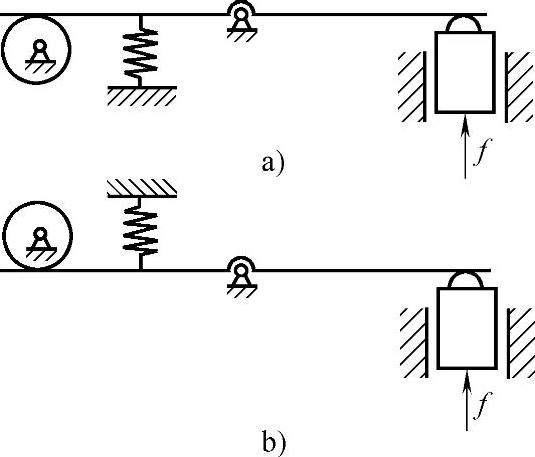
图6-111 凸轮机构磨损量的抵消原理
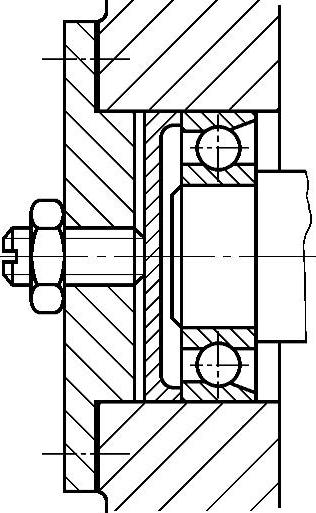
图6-112 轴承的间隙调整结构
(3)利用误差均化原理来提高精度的方法 误差均化原理指出:如果在机构中有多个作用点对同一个零件的运动起约束作用,则该零件的运动精度会高于任何一个作用点单独作用时的精度。如图6-113所示螺旋测量仪的测量误差与螺距实际误差的对比。
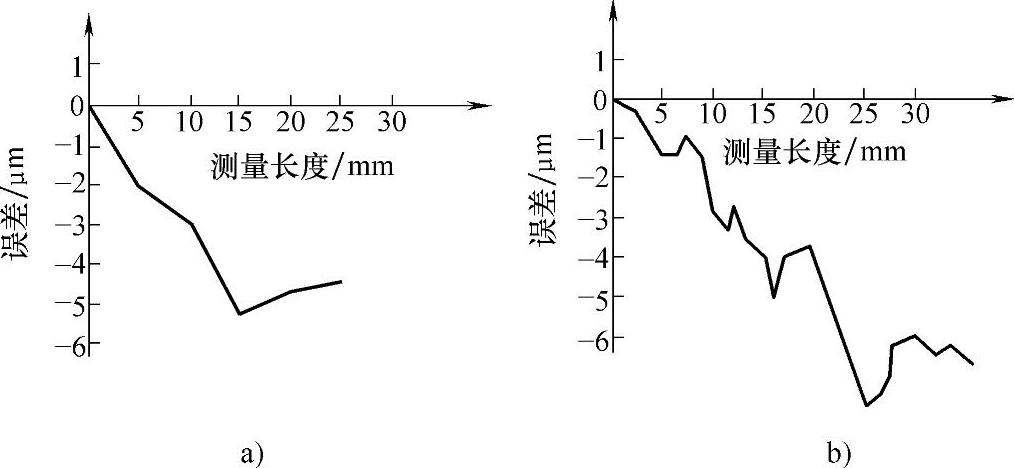
图6-113 螺旋测量仪的测量误差与螺距实际误差的对比
a)测量误差 b)实际误差
在测量时,由于螺母上有多圈螺纹同时起作用,结果使得测量误差(即螺母的运动误差)要小于螺纹本身的实际螺距误差。利用该项原理设计的双蜗杆驱动机构如图6-114所示。

图6-114 双蜗杆驱动机构
在图6-114b中:曲线A、B分别表示两个蜗杆单独驱动时工作台的回转精度;而当两个蜗杆同时驱动时,在a-b-c段由蜗杆A起作用;而在c-d-e段蜗杆B起作用。因此,减小了误差。所以,由于误差均化作用,使得蜗轮的运动误差小于任何一个蜗杆单独驱动时的误差。

图6-115 多级机械传动系统
(4)利用误差传递规律来提高精度的方法 误差传递规律表明:在一个由多级传动机构所组成的传动系统中,各级机构的误差也会向后续机构传递。如图6-115所示为多级机械传动系统。图中,第一级输入角速度ω1,其输出的角速度ω2除了包括对ω1的变换以外,还包括本级传动所产生的误差δ1,即
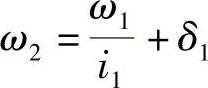
同理,第二级的传动输出为
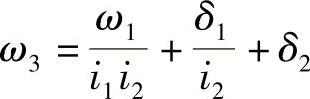
最后一级输出为

由此可见,在输出的角速度中,包含了各级传动所产生的误差的叠加。但是,各级误差对输出误差的影响是不相同的。由最后一级输出公式可知:如果将最后一级的传动比i3选择得较大一些,则可以使得前面各级传动所产生的误差对于最后的运动输出基本不起作用。因此,只要为最后一级的传动零件选择较高的精度(即选择较小的δ3),即可提高整个传动系统的传动精度。
(5)合理配置系统精度的方法 先观察一个实例,如图6-116所示的前、后轴承精度对于主轴精度的影响。图中:前支点误差δa所引起的主轴的前端误差为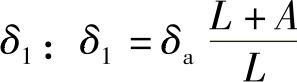 ;后支点误差δa所引起的主轴的前端误差为
;后支点误差δa所引起的主轴的前端误差为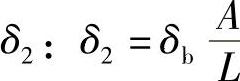 。
。
显然,前支点误差δa对于主轴前端精度的影响比后支点误差δb的影响大得多。因此,在主轴结构设计中,将前支点设置具有较高精度的轴承。
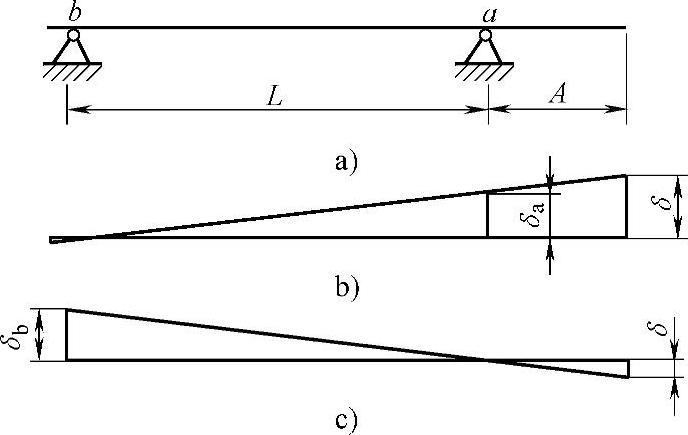
图6-116 前、后轴承精度对于主轴精度的影响
从上述实例可知:系统的精度受到其内部各个环节精度的综合影响。因此,在结构设计中,应为不同的位置设置不同的精度,尤其应为敏感位置设置较高的精度,以达到用经济的方法获得较高的整体精度的效果。
(6)选择较好的近似机构以减小其原理误差的方法 有时为了简化结构需要采用近似机构,但这会引入原理误差。所以,为减小原理误差,应尽量选择近似性较好的近似机构。例如图6-117所示为两种近似机构的比较。图a为正切机构,其手轮旋转角ϕ与摆杆的摆角θ之关系为: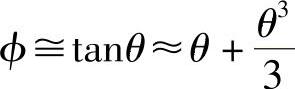 ;图b为正弦机构,其手轮旋转角ϕ与摆杆的摆角θ之关系为:
;图b为正弦机构,其手轮旋转角ϕ与摆杆的摆角θ之关系为: 。可见,正弦机构的原理误差比正切机构的原理误差要小一半。而且,其螺纹间隙引起的螺杆摆动基本不影响摆杆的运动。因此,采用正弦机构可以获得更高的传动精度。
。可见,正弦机构的原理误差比正切机构的原理误差要小一半。而且,其螺纹间隙引起的螺杆摆动基本不影响摆杆的运动。因此,采用正弦机构可以获得更高的传动精度。
(7)采用有利于施工的结构来提高精度的方法 任何结构的原始精度都是通过工艺过程来实现的。如果采用有利于施工的结构(包括考虑加工要求、检验要求和减小装配变形等项内容),就有利于提高精度。
1)考虑加工要求。例如图6-118所示为有利于同一道工序加工的结构。为保证两端轴径具有较高的同轴度,要求能够在同一次装卡中完成对于两端轴径的加工。显然,图a所示结构达不到此项要求;而图b所示结构,在其左端增加了一个工艺性轴段,因此可以实现一次性装夹中完成对于两端轴径的加工,确保了高精度的要求。
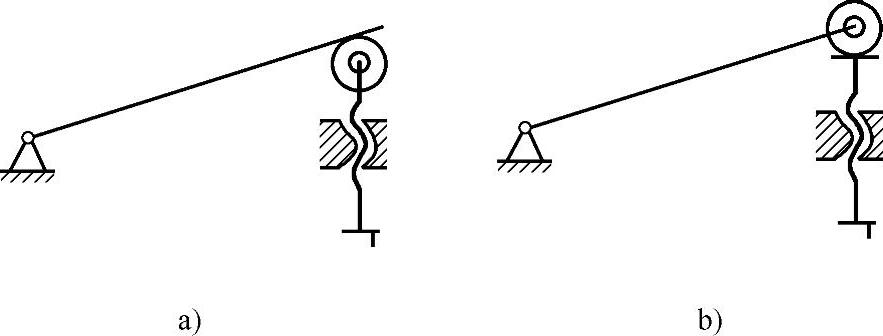
图6-117 两种近似机构的比较
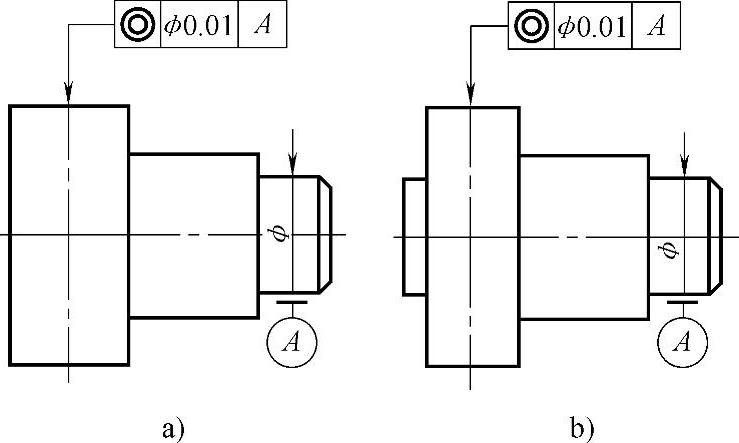
图6-118 有利于同一道工序加工的结构(https://www.xing528.com)
2)考虑检验要求。必须充分考虑检验工艺与检验工具的要求,使得每一项技术要求都可以被检验。在图6-119所示的结构中,由于台阶高度太小,无法检验,应加高台阶以确保测量。又如图6-120所示的三项尺寸中,仅有A1参数可以直接测量。而参数A2与A3均无法直接测量,不利于检验。
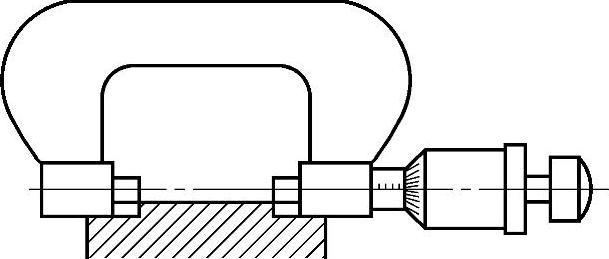
图6-119 不利于测量工具使用的结构
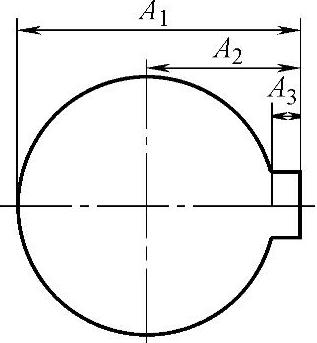
图6-120 尺寸的可测量性
3)减小装配变形。必须充分考装配对于零件精度的影响。图6-121为相对于装配变形的两种不同结构的比较。图a所示结构中,如果作为安装基准的下平面不平,装配后会引起导轨工作表面(上表面)的变形,对精度不利;如果改为图b的结构,则可消除装配对于精度的影响,有利于导轨精度的提高。
(8)灵活运用阿贝原理来提高精度的方法 阿贝原理是测量仪器和量具设计的指导性原则,即:欲使量仪给出正确的测量结果,必须将仪器的读数线尺安放在被测量尺寸的延长线上。如图6-122b所示之外径千分尺(即螺旋测微仪)的结构符合阿贝原理,故可实现高的测量精度;而图a所示之游标卡尺的结构不符合阿贝原理,所以不能达到较高的测量精度。
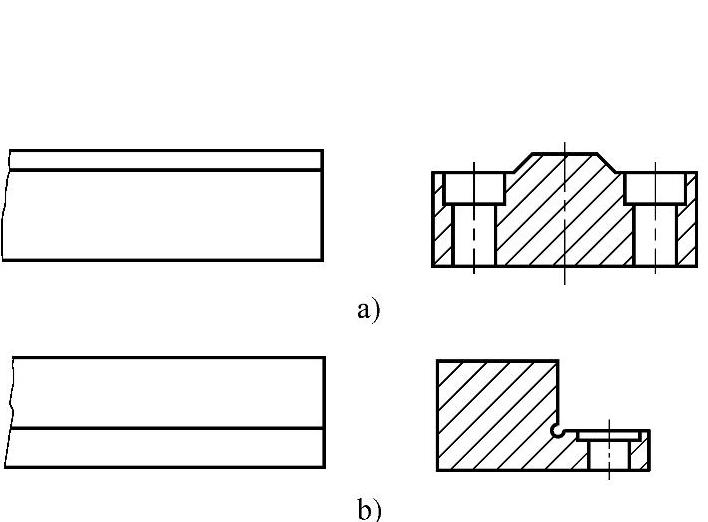
图6-121 相对于装配变形的两种不同结构的比较
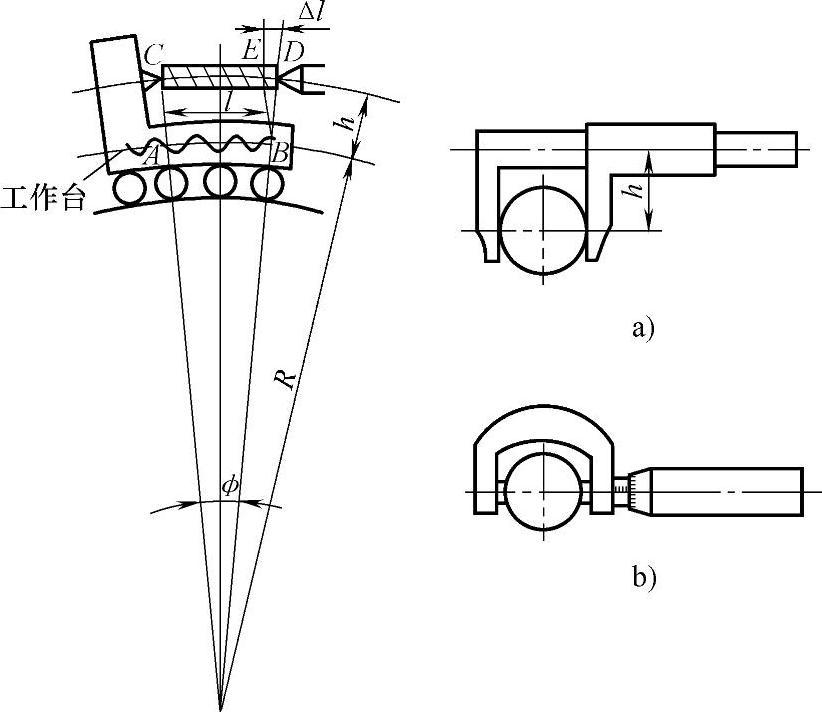
图6-122 阿贝原理示意图
a)不符合阿贝原理 b)符合阿贝原理
现将阿贝原理分析如下(图6-122左图):假设由于导轨和丝杠误差使得工作台沿着丝杠及导轨作圆弧运动,又因测量线是沿丝杠而与工件不在同一条直线上,工件长度为CD,丝杠长为AB,故其测量误差为
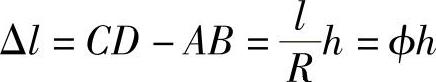
可见,欲使Δl=0,只有使得ϕ=0或h=0,才能消除此项测量误差。h=0即意味着“必须将仪器的读数线尺安放在被测量尺寸的延长线上”,于是阿贝原理得到证明,否则应使ϕ=0,即要求导轨没有角运动,或格外进行补偿。
由上述分析可知,要想符合阿贝原理,即保证被测工件与读数线尺共线,则该量仪的长度尺寸就会非常之大。所以要完全满足阿贝原理比较困难。在工程实际中,往往是采取补偿措施,尽量缩小阿贝原理误差。
(9)通过减少回程误差来提高精度的方法 回程误差是指由于组成工作机构的运动副均存在间隙,故当改变其运动方向时(即回程),由于零件工作表面发生变换,使得被动件的运动方向改变滞后于主动件,而导致回程误差的产生。所以,减少回程误差的主要方法是减小、调整或消除运动副的间隙。
图6-123为卧式车床溜板箱进给螺纹的间隙调整结构。
其中进给螺母被切分为两部分,并可实现间隙调整。先松开左侧固定螺钉,拧紧中间的调整螺母,使楔块上移,同时推动左侧螺母左移,使得螺纹间的作用间隙减小,达到减小回程误差之目的。若将楔块改为弹簧,也可起到减小或消除螺纹间隙的作用。
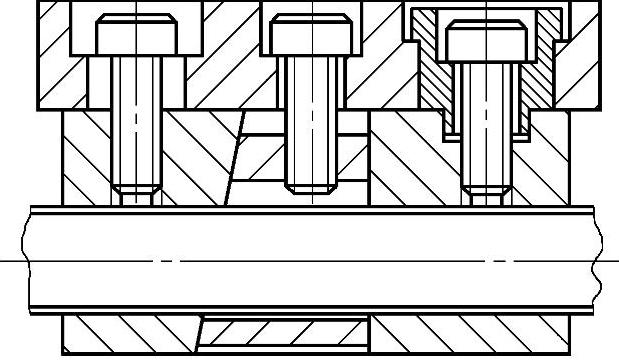
图6-123 卧式车床溜板箱进给螺纹的间隙调整结构
图6-124所示为消除齿轮啮合间隙的结构。
其中,将原有齿轮沿齿宽切分为两半,两半齿轮通过弹簧联接并可相对转动。由于弹簧的作用,可使得两半齿轮分别与相啮合齿轮的不同齿侧相接触,因而消除了啮合间隙,并可及时补偿磨损引起的间隙变化。
图6-125所示为千分尺的传动系统。当表头移动时,固定于齿轮z4′上的“蜗卷弹簧”储能,当表头改变运动方向时,各个齿轮也改变转动方向,但因“蜗卷弹簧”的作用,使得原来的主动齿轮变为被动齿轮,因此,各个齿轮的工作齿侧不变,所以,虽然存在齿侧间隙,但不会产生回程误差。

图6-124 消除齿轮啮合间隙的结构
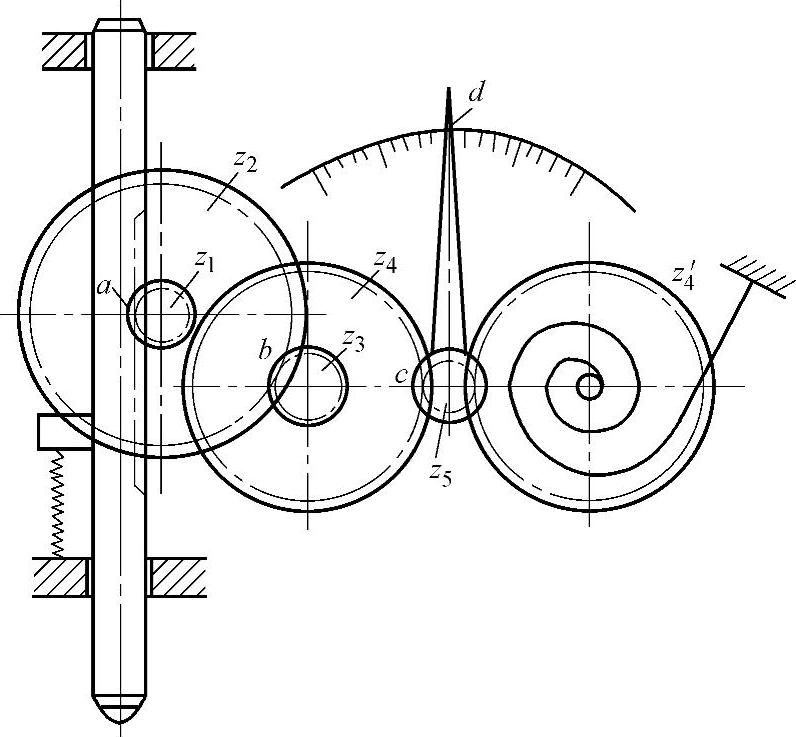
图6-125 千分尺的传动系统
(10)选择适当的材料与补偿温度误差的方法
1)选择适当的材料。选用尺寸稳定的材料有利于提高结构精度。如用花岗岩制造平板角尺等精密工具。由于它经过百万年的天然时效处理,其内应力已经完全消除,几乎不会变形,且加工方便,容易得到很小的表面粗糙度,不生锈,对温度不敏感,绝缘性好,抗振,阻尼系数大,价格便宜。其主要缺点是脆性大。近年来,国内外多采用花岗岩作为精密机械的基础件,如三坐标测量机的工作台、立柱、导轨、横梁等,尤其用作空气导轨的基座和工作台最为合适。
2)补偿温度误差的方法。补偿温度误差的实例如图6-126所示的铝合金机座。铝合金机座的线胀系数比联接螺栓(普通碳钢)大,为了补偿由于温度变化引起的变形差异,在其中间增加一个用殷钢(含镍36%)制作的套筒。由于殷钢的线胀系数仅为普通碳钢的1/10,因此,只要正确选择长度尺寸l1、l2、l3时,就可以完全消除温度变化而引起的尺寸误差与应力。关于长度尺寸关系的计算方法:图6-127所示为量具与工件尺寸,图6-128所示为补偿温度误差的量具尺寸。

图6-126 补偿温度误差实例(铝合金机座)
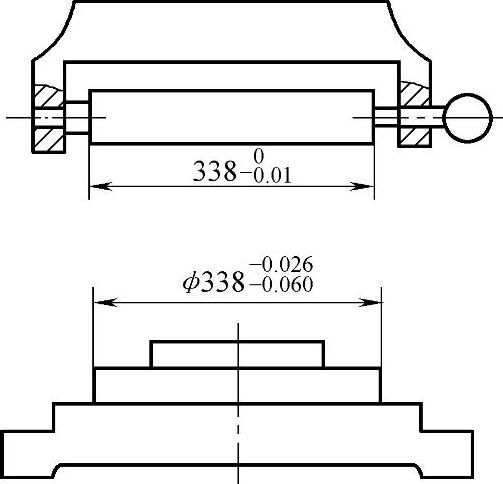
图6-127 量具与工件尺寸

图6-128 补偿温度误差的量具尺寸
在图6-129中,某个材料为铸造镁合金的零件被测量尺寸为338,其线胀系数是碳钢量具的2.4倍。而加工车间从冬天到夏天的温度变化在5~35℃之间,因而温度误差远远超过了零件的公差范围。必须进行温度误差的补偿。
图6-129 搭扣紧固设计
图6-128是能够进行温度误差补偿的量具,其尺身长为La,顶杆长为Lc,工件长为Lb。三者分别用三种线胀系数αa、αb、αc的材料制成,在环境温度T=20℃时满足如下关系:
La=Lb+Lc (6-1)
则当温度为t时三者的尺寸分别为:L′a、L′b、L′c,计算如下:

设此时仍能满足

式(6-3)揭示出了温度误差补偿的基本原理:即“用一种线胀系数较小的材料(T8A),来补偿线胀系数较大的材料(ZM5)的温升引起的伸长,而使得它们之和与一种线胀系数为中间值的材料(LY12)的温升引起的伸长相等,从而消除了温度变化所引起的误差。
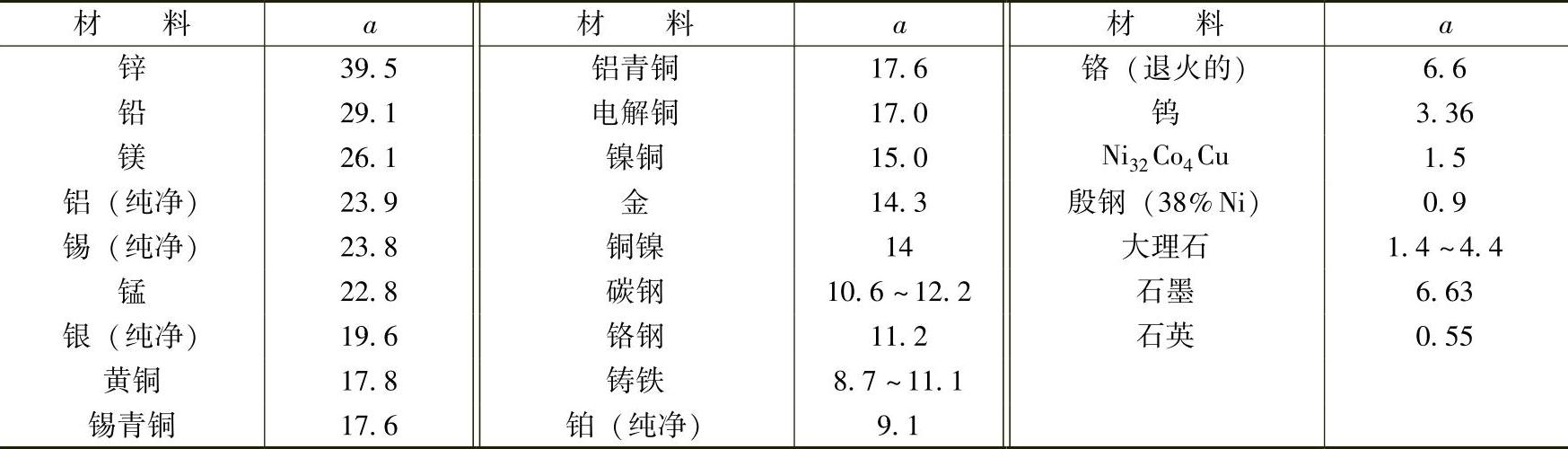
表6-10给出了常用材料的线胀系数。
表6-10 常用材料的线胀系数
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




