功能结构分析方法的应用

功能结构分析有多种具体方法，如功能展开分析法、结构模型解析法以及多变量解析法等。

1.功能展开分析法

功能展开法是以二维坐标方式，将产品的功能和产品设计要点进行展开，以找出两者的关系。横轴表示功能以多阶形式展开的结果，纵轴则表示设计应注意的要点。两者的关系是用二维交叉点来表示。功能展开的级别要以产品的复杂程度而定，通常是展开到3～4级。

【案例5-6】用功能分析法分析船舶的功能结构体系图

图5-20是用此种方法分析船舶的功能结构体系结果。

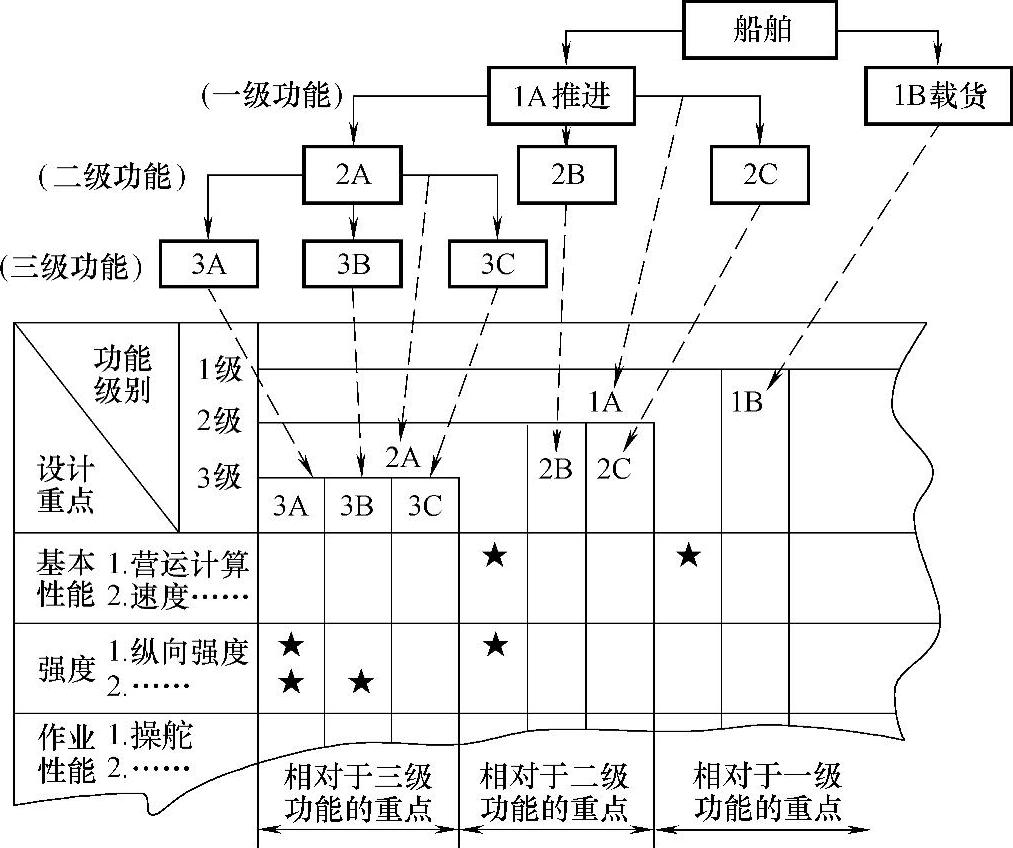
图5-20 用功能分析法分析船舶的功能结构体系图

注：★表示设计中的重点。

下面再给出两个应用功能分析法的实例。

（1）如何决定设计重点项目

【案例5-7】用功能分析法决定船用大型内燃机设计重点

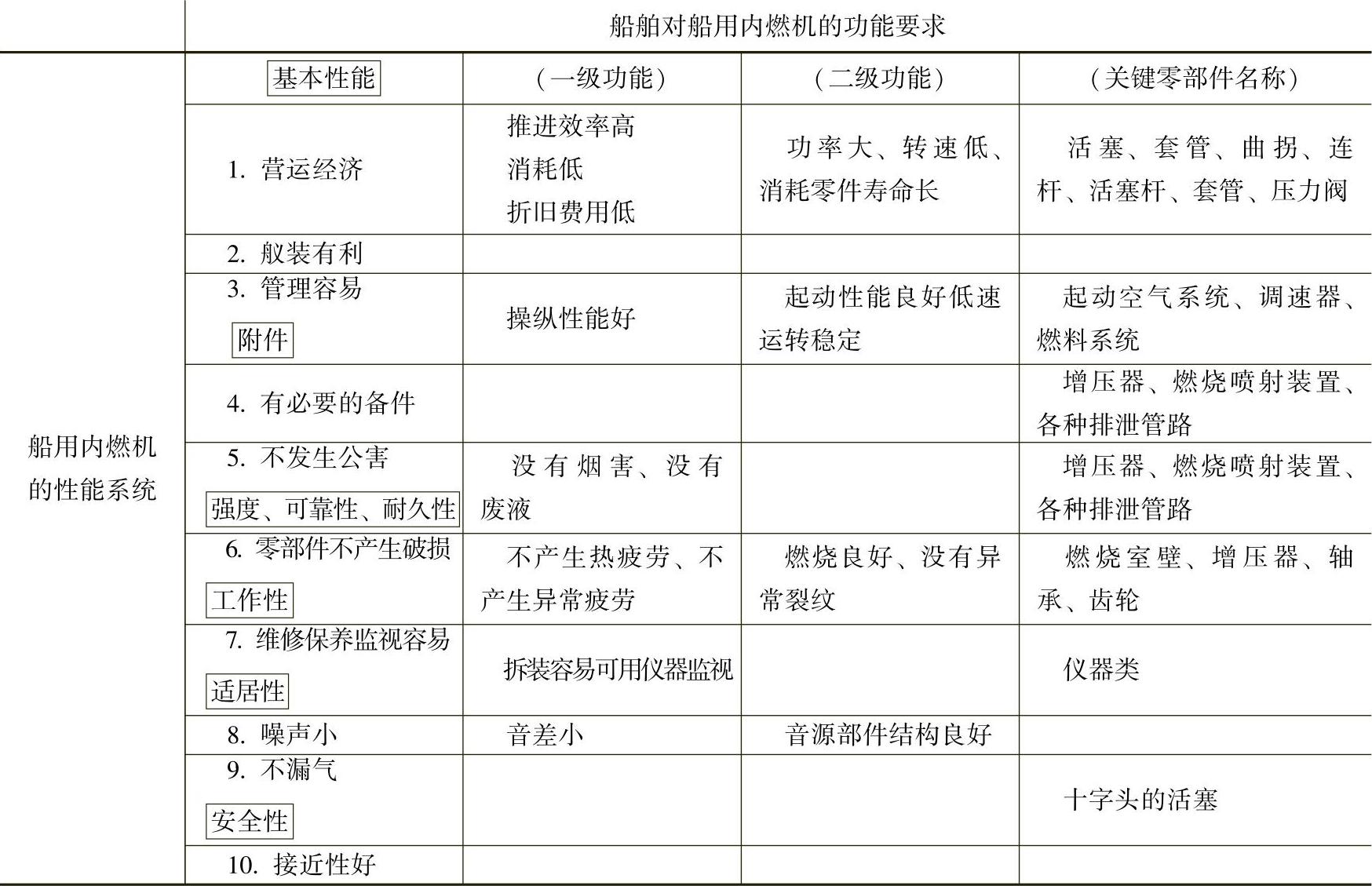
表5-6是决定船用大型内燃机设计重点的实例。船用大型内燃机是船舶的心脏，是属于船舶的一个上位子系统。设计船用大型内燃机时既要使其功能满足船舶的需要，又要满足内燃机自身的功能要求。通过功能展开法，就便于将其重点项目明确而清晰地反映出来，进而确定正确的设计思想。

（2）如何防止设计中遗漏某些功能项目 防止设计中遗漏某些功能项目的最好方法，是多进行同类已有项目的总结分析，找出经常容易遗漏的地方。同时，应注意各个专业组互相衔接的作业点。

表5-6 决定船用大型内燃机设计重点的实例

【案例5-8】用功能分析法在舵机设计中防止遗漏功能项目

表5-7给出了此种方法在舵机设计中的应用实例。表中将设计中经常容易疏忽和遗漏的功能用功能与结构的交叉点来表示。以防设计中遗漏功能的发生。

表5-7 在舵机设计中用“功能分析法”防止遗漏功能项目

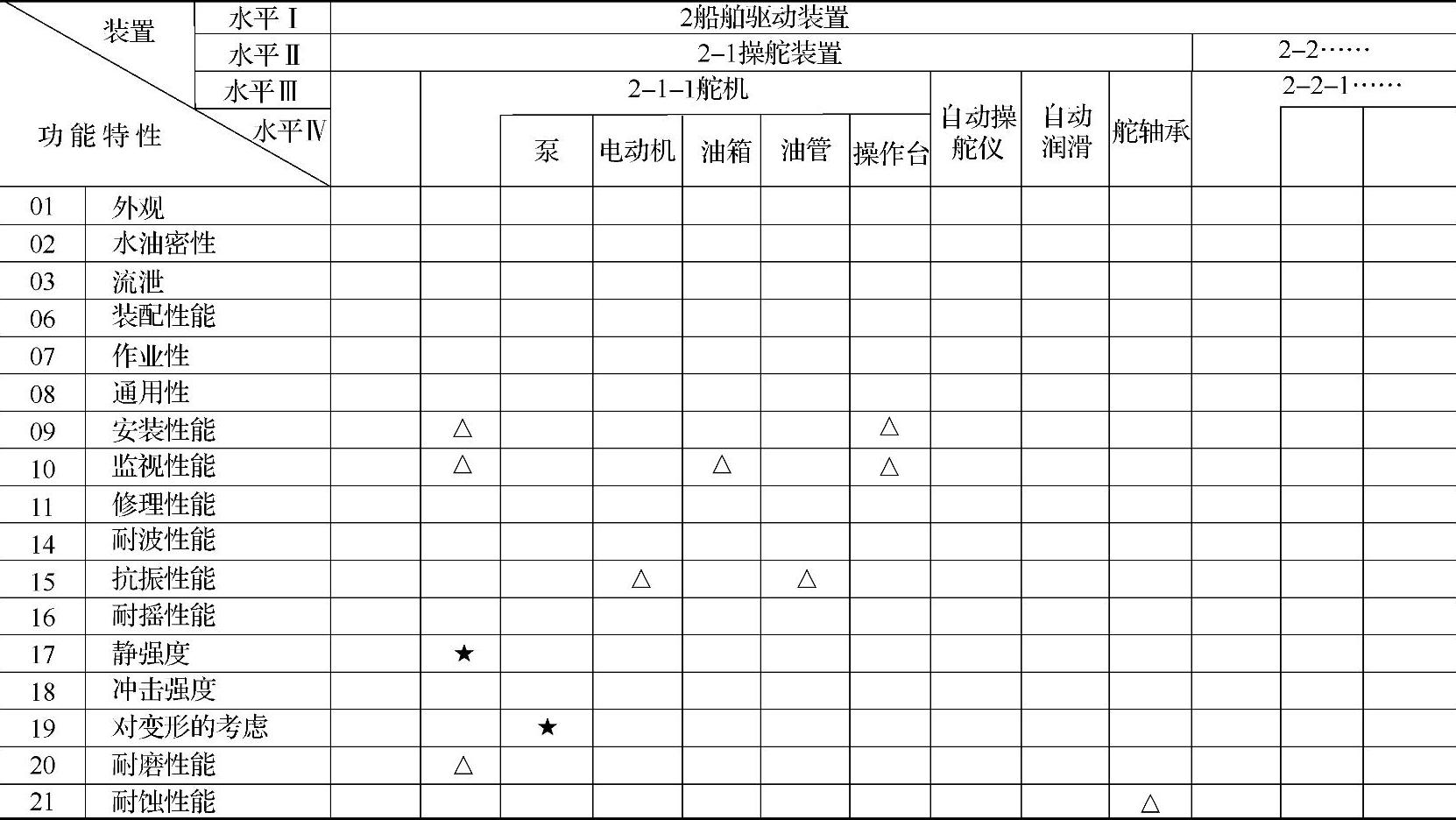
注：△—表示过去设计中，经常容易发生的小问题；★—表示过去设计中，经常容易发生的大问题。

功能分析法的优点是比较直观，特别适用于相对简单的系统。但对于一些比较复杂的大型系统而言，使用功能分析法就十分困难了。这时就要借助下面的结构模型解析法了。

2.结构模型解析法（ISM）

结构模型解析法可以确定复杂系统中大量元素之间的因果关系、上下关系和大小关系，并能够将复杂的系统分解成为条理分明的多级递阶结构形式图。因此，近年来它在城市规划设计、区域环境规划以及复杂的企业计划与发展决策等领域获得了广泛的应用。

结构模型解析法的原理是：通过有向图和相邻矩阵的有关运算，得到可达性矩阵，然后加以分解，从而将复杂的系统分解成为多级递阶结构图。下面举例对其原理和分析方法加以说明。

【案例5-9】石油冲击造成造船业不景气的各种原因间的关系分析

试分析石油冲击造成造船业不景气的各种原因间的关系，并绘制其多级递阶结构图，同时预测船舶设计中应注意的问题。

1）问题的表达以及有向连接图、相邻矩阵及可达性矩阵的建立

①建立有向连接图。表5-8给出了经随机采样得到的船舶业受石油冲击后出现不景气的各种原因。如果分析这些原因之间的因果关系，便可得到表5-9船舶业受石油冲击后出现不景气各种原因间的因果关系。在表5-9中，以“列”表示原因项，而以“行”表示结果项。如果在原因项与结果项之间存在着因果关系，则在其交叉点处用“1”加以表示。根据表5-9，便可建立有向连接图，见图5-21。在该图中，构成系统的各个元素用节点i表示，而元素间的因果关系则以带有箭头的线段表示，故称有向连接图。

表5-8 船舶业受石油冲击后出现不景气的各种原因

表5-9 船舶业受石油冲击后出现不景气各种原因间的因果关系

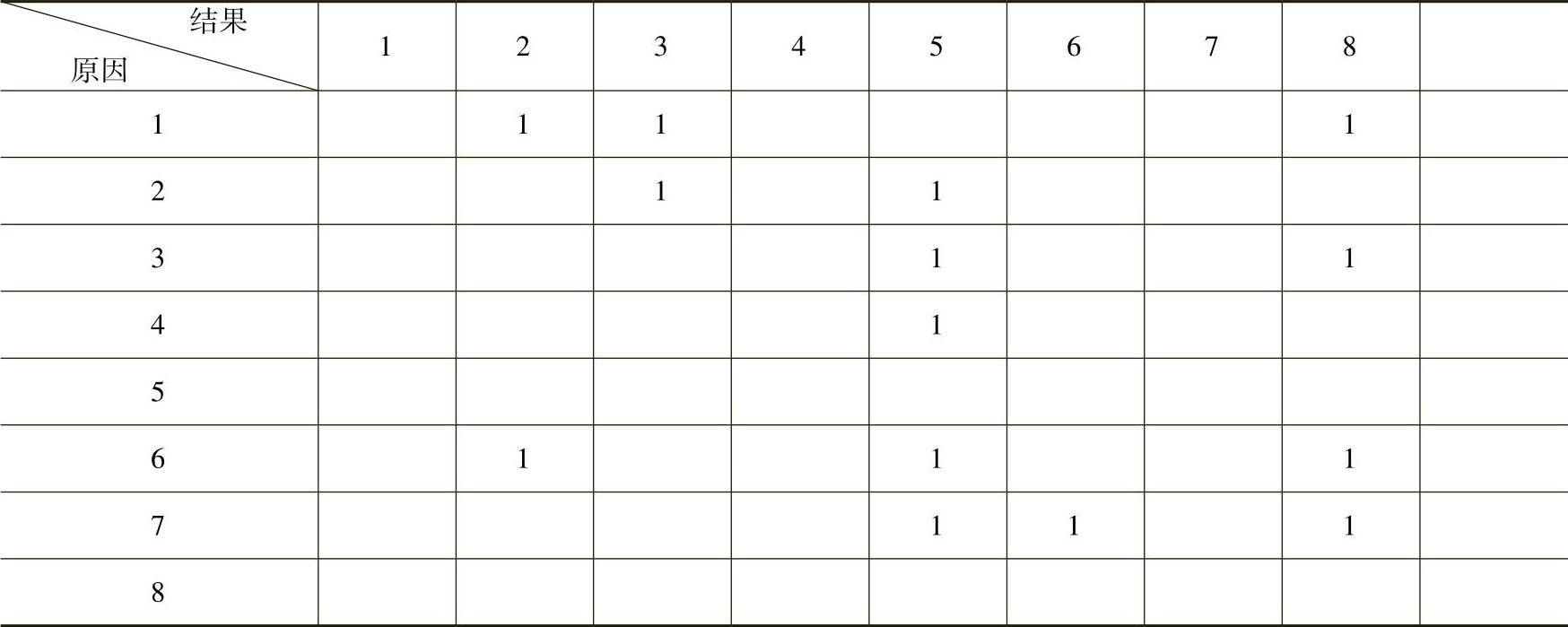
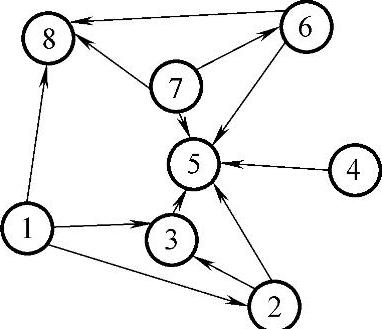
图5-21 有向连接图

②建立相邻矩阵A。所谓相邻矩阵就是用来表示有向连接图。图5-21中各个元素间连接状态的矩阵，通常称为相邻矩阵A。其元素a_ij定义为

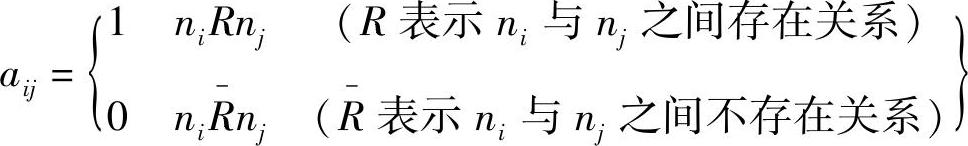
因此，表5-9所给出的因果关系可以用相邻矩阵A来表示如下：

相邻矩阵也称为系统的要素间因果关系的二值矩阵。可见，其中的1与表5-9中的1是成一一对应关系的。

③建立可达性矩阵M。可达性矩阵是反映有向连接图各节点间，通过一定路径可以达到的程度。它的建立方法是：

a）首先建立一个新矩阵A₁：使A₁=A+I；（A+I）表示将矩阵A加一个单位矩阵，即只将对角线的元素加1。

A₁具有如下特性：当其中元素a_ij=1时，则表示节点i到j可以直接达到。

但是，A₁还不是可达性矩阵，还要继续以下运算。

b）建立可达性矩阵M。下面依次进行A₁的自乘运算，即进行（A+I）2，（A+I）3…的运算，可得(www.xing528.com)

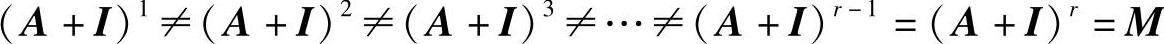
即：

应当说明，以上从不等式到等式的过程就是建立可达性矩阵的过程：依次进行A₁的自乘运算，若经过（r-1）次自乘运算变换后，能够得到两个完全相同的矩阵，则该矩阵便是可达性矩阵M。所以，在这里应将等式理解为两个完全相同的矩阵。

由上式可知，当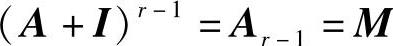时，M即为可达性矩阵。它表示：在M中，若要素I=1（即在原矩阵中增加对角线均为1的元素），则在节点之间，可以用多至（r-1）条路径来达到。

在本例中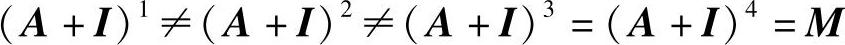：，即

2）可达性矩阵的分解

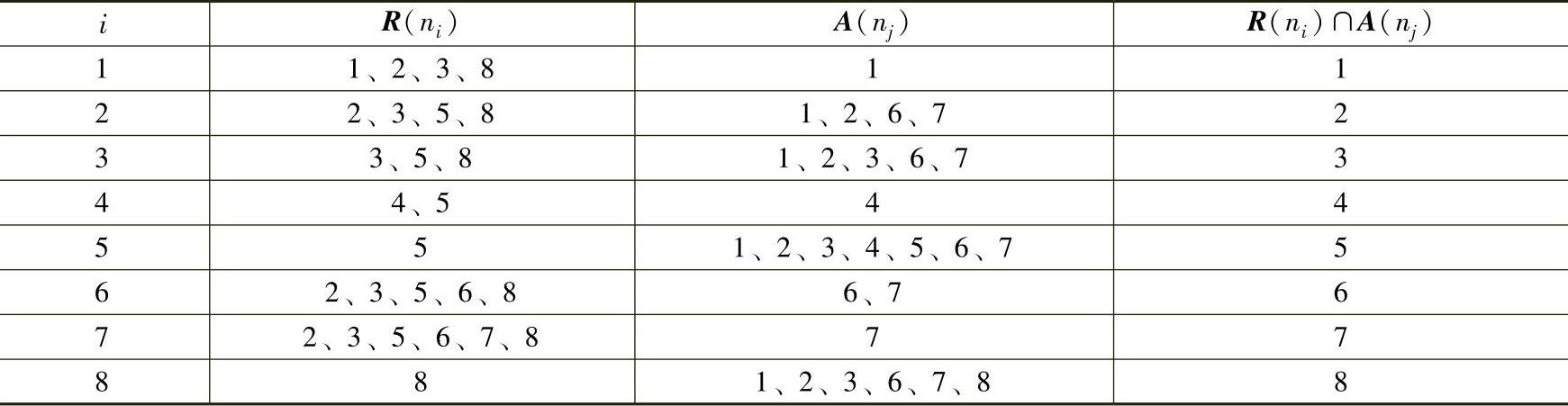
①建立可达性矩阵M的可达性集合、先行集合和共同性集合，见表5-10，三者的定义如下：M的可达性集合：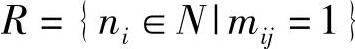

M的先行集合：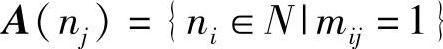

M的共同性集合：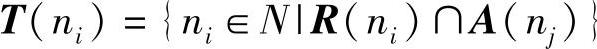

表5-10 M的可达性集合、先行集合和共同性集合

②求多阶结构模型的第一级项及简化矩阵M′：

a）在表5-10或图5-21中的“i=5，8”两项，是属于不能达到其他任何项目的项，是在多级递阶结构中的最上位的项目，即为多阶结构模型的第一级项。

b）从M中，将“i=5，8”两项所对应的行与列去掉，便可得到简化矩阵M′，即

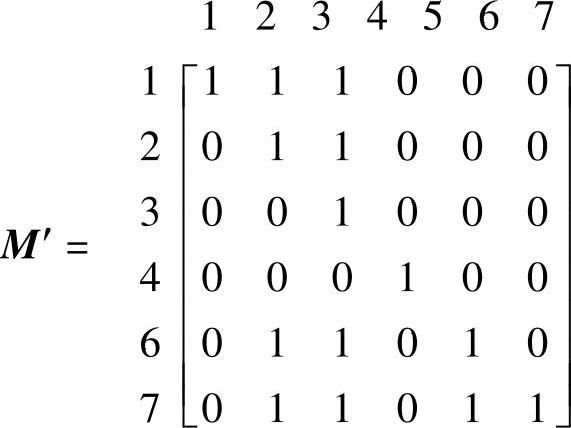
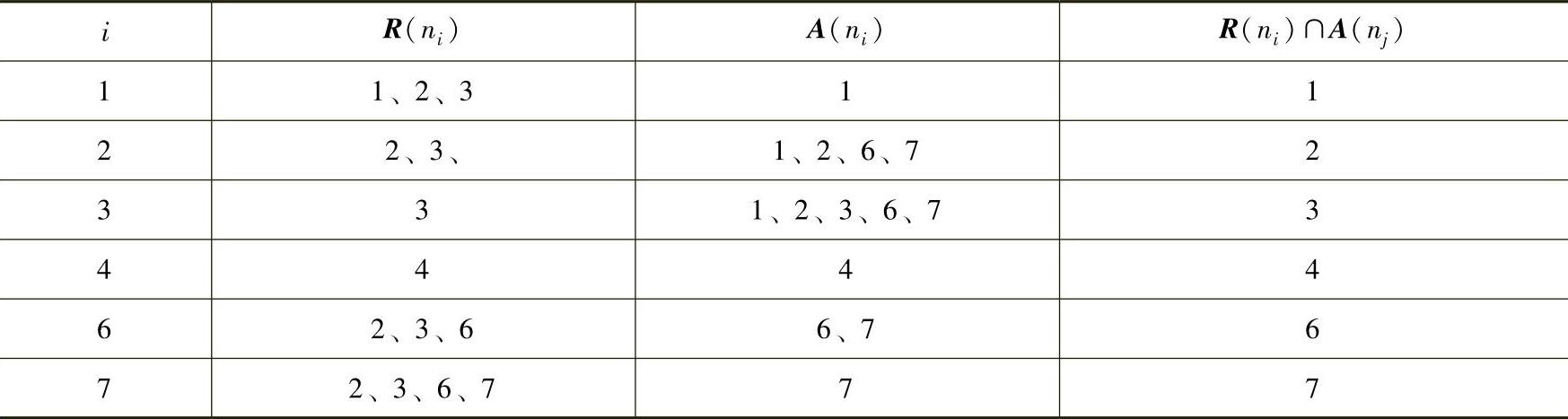
c）再建立简化矩阵的M′的可达性集合、先行集合和共同性集合表，见表5-11。

表5-11 简化矩阵的可达性集合、先行集合和共同性集合表

d）用同样的方法求多阶结构模型的第二级项（i=3，4）及简化矩阵M″、第三级项（i=2）及简化矩阵M‴。

e）重复上述操作得到第四级项（i=1，6）和第五级项（i=7）。

3）结构模型的建立

①首先将上述分析所得到的各级项结果，绘制成图5-22的多级递阶结构图。

②然后再将其转换成图5-23的结构模型。

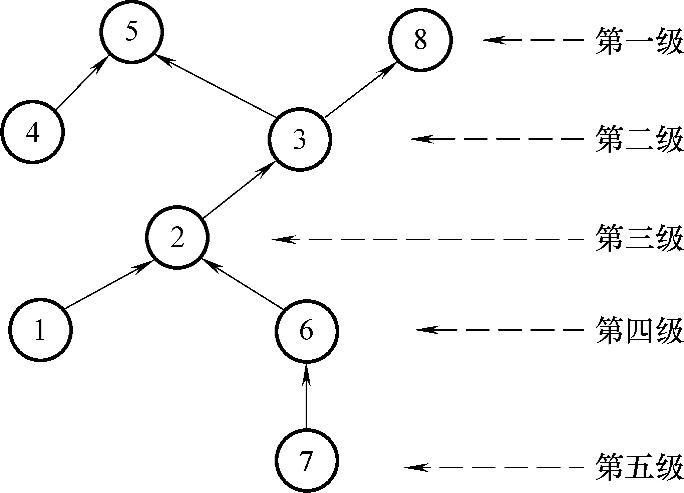
图5-22 多级递阶结构图

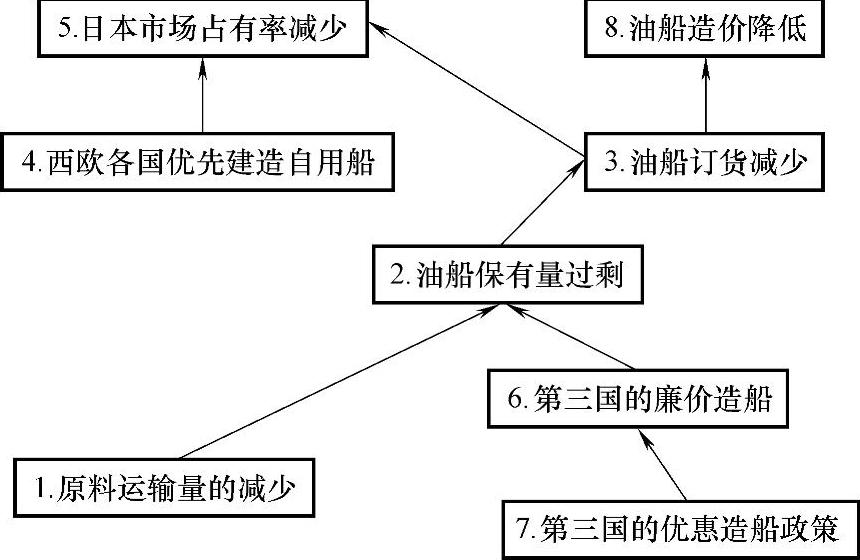
图5-23 结构模型

结构模型非常清晰地反映出系统的各个要素的关系及其影响程度。如本例，使我们对石油冲击造成造船业不景气的原因以及相互关系有了比较清楚的认识，其中的第三国的优惠造船政策产生的影响程度最大、且波及面也最广。这些对预测造船业的发展是很有帮助的。

归纳以上分析，可得到结构模型解析法（ISM）的工作程序：

1）提出问题，确定组成系统的元素集合，元素编号，列出明细表。

2）建立相邻矩阵：先组织相关人员讨论分析，找出各个元素间两两的对应关系，建立因果关系表，再以关系表为基础，建立相邻矩阵。

3）经过一定的运算后，求得可达性矩阵。

4）将可达性矩阵进行分解和检出，得到多级递阶结构项。

5）根据多级递阶结构项绘制多级递阶结构图和结构模型图。

3.多变量解析法

多变量解析法包括主成分分析法、类别分析法、数量化模型等多种方法。现广泛用于从众多基础统计数据中，找出构成问题的主要因素的情况。

【案例5-10】用主成分分析法计算集装箱船各主要影响因素

以往的船舶设计资料多按照排水量、长度、宽度等进行分类。这些方法不完全合理，因为没有表明要素对功能的影响程度与区分主次。现以集装箱船为例，研究主成分分析法在船舶设计中的应用。图5-24a是用主成分分析法计算表征集装箱船特征的各个主要因素的结果。

首先，作为第一主成分，被计算出来的是包括表征船舶运输力的功能的各个因素，如排水量、集装箱数、载重量等，其贡献率就高达69%。

其次，再看第二主成分，见图5-24b。对其影响最大的因素是甲板上集装箱层数，它是表征集装箱船特有形态特征的参数，指其是两层集装箱船，还是三层集装箱船。

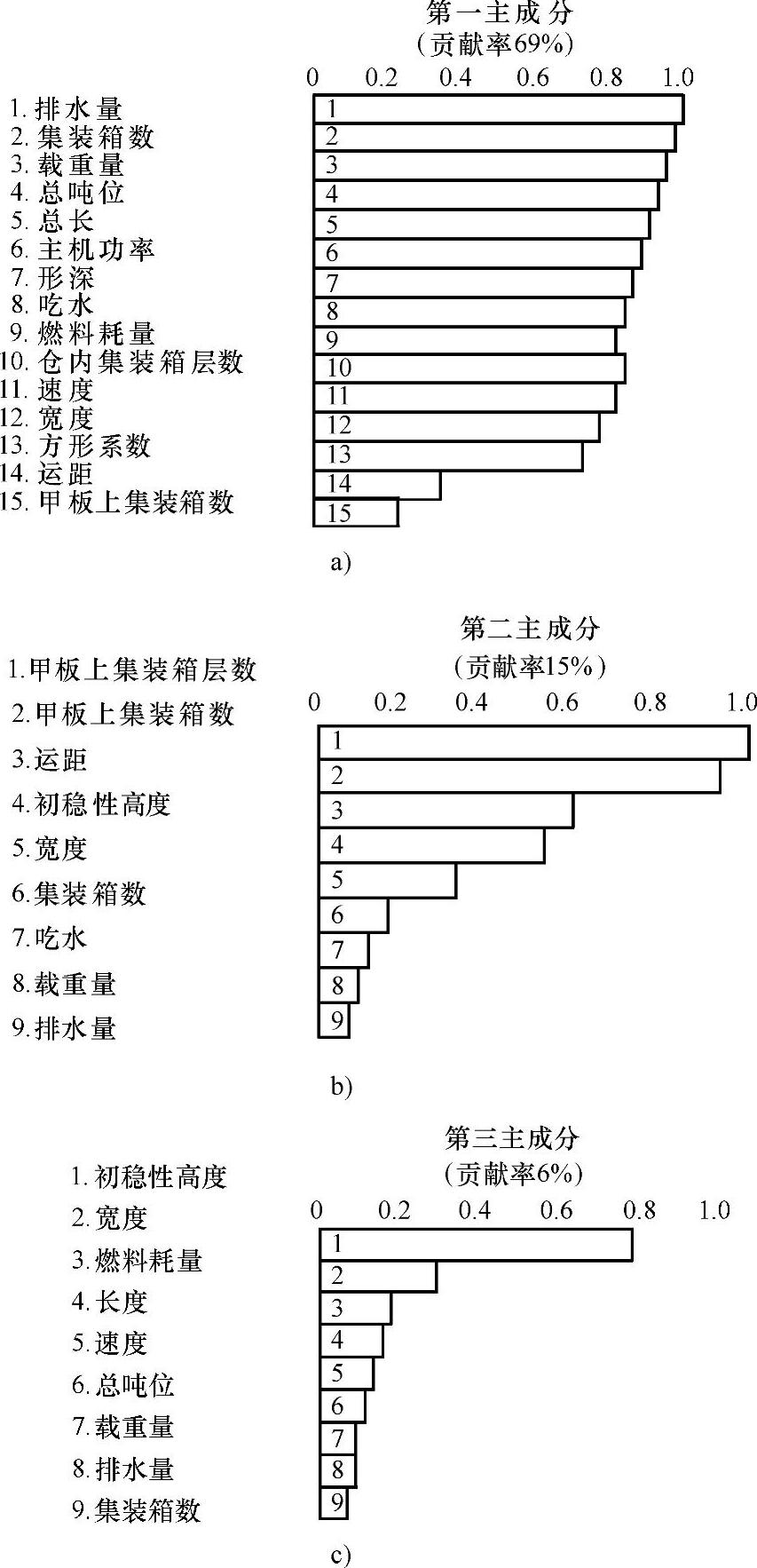
图5-24 用主成分法分析计算集装箱船各主要影响因素

如图5-24c所示，第三主成分是表征与稳定性有关的因素，其中以初稳性高度影响最大。