相似理论及其在实践中的应用

反求工程依据的基本理论是相似理论，现说明如下：

（1）相似理论概述 相似理论是研究相似现象的性质及其规律的理论，主要是研究物理现象之间的相似条件、相似准则及有关的相似定理，并求出相似准则之间的函数关系式。有了相似理论，使试验不必对每个现象逐一进行，只要用相似的模型进行试验即可。相似理论也是一种完整地研究、整理和综合实验数据的方法论。根据相似理论，可将影响现象变化的全部物理量，适当地组合成几个无量纲的相似准则，然后把这些相似准则作为一个整体，来研究各物理量之间的函数关系。这就使试验次数大大减少，实验工作的设置和费用也大为降低，而且扩大了实验结果的应用范围。系统相似、尺寸性能参数成一定比例关系的系列产品为相似产品系列。在基型产品的基础上，用相似理论就可进行某个相似产品或相似产品系列的设计，这种相似设计法直接利用量纲原理和相似比关系，可以高效地得出计算结果。

相似理论作为一门在机械设计领域应用的方法学，统称为相似设计方法。它可以解决模型试验如何进行，系列产品如何设计以及计算机仿真的原理等问题，有着广泛的应用范围。由于经济上的考虑及技术方面的限制，对原型进行试验会遇到很大的困难。因此，很多机械性能或自然现象机理的研究，是在实验室条件下以实物模型来进行的。但在试验条件下，应该怎样选择参数，才能使模型试验的现象能真实反映原型的规律，如何将试验模型时所得数据，换算到实物原型上去，是必须要解决的问题。这时，就需要用到下述相似理论。

（2）相似定理和相似准则 相似定理。如果两个现象的单值条件相似，并且从单值条件中所引出的相似判据相等，则这两个现象相似。单值条件是指把具体现象从一群现象中区别出来的条件。相似准则：由现象的特征量所组成的无量纲数。在模型试验中，必须先得到两个相似物体的相似数及相似准则（判据）。可以根据各种单项相似的情况，求得相似准则。相似是指表述一组物理现象的所有物理量，在空间相对应的各点和在时间上相对应的瞬间，各自互成一定的比例关系。这种相似关系主要有：几何相似、时间相似、运动相似、动力相似、边界条件（周围介质相互作用的条件，如流体在管中流动，其入口和出口处的压力、速度以及管壁处的速度）相似、物理参数相似等。

1）几何相似。两个结构相似的物体中，任何相当的几何尺寸的比值为常量，则为几何相似。如两个三角形物体，其三个边分别为x、y、z与x′、y′、z′三个尺寸要素，则对应的比值为：x′/x=K_x，y′/y=K_y，z′/z=K_z，几何相似即：K_x=K_y=K_z=常数。这是几何相似最主要的特征。在大多数模型试验中，只要按比例制造物体的外廓就够了。但在某些特定的试验研究中，可能有进一步的几何相似要求，如在附面层稳定性试验研究中，还要求表面粗糙度相似。

图4-18 时间相似

2）时间相似。时间相似（图4-18）是指对应的时间间隔互成比例。或者说，若两系统的对应点或对应部分，沿着几何相似的路程运动达到另一个对应的位置时，所需要的时间比例是一个常数。即满足下式，则为几何相似：

3）运动相似。物体各对应点处质量、运动、速度成比例，即运动相静态与动态运动速度分别可为：

变速运动：

匀速运动：

式中 u、v、w、u′、v′、w′——两物体的速度；

t——时间。

若完成运动的时间的比值为常数，即：K_t=t′/t=τ=常数，则

同理：

所以可得速度相似数为

同理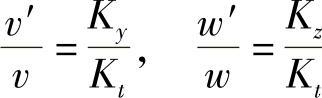：均为常数

所以用通式表达为

4）动力相似。物体对应点处的质点上作用着同一性质的力，并且有同一比值，即为动力相似。若两物体作用同一性质的力，分别为F=ma与F′=m′a′。则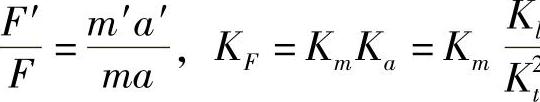：此即动力相似数。

以上是相似模型必须满足的基本相似准则.其他的相似准则判据则是在此基础上，根据不同现象的模型试验来加以确定的。这往往是最关键、最重要，但却是最困难的。

5）量纲分析。当我们研究某一现象时，首先，要引进表征该现象的状态的一些特征量。例如，当研究力学过程时，要考虑力、密度、速度等。其次，要引进测量这些量的单位，使我们可以用一些数值来表示这些特征量。特征量数值的大小与所选的量度单位有关。不同特征量之间存在着由物理定律或这些量的定义本身所确定的关系式。因此，宜先规定那些彼此独立的特征量的量度单位，而其余各量的量度单位，即由这些独立的量度单位所决定。这些独立量的量度单位称为基本单位。其余量的量度单位称为导出单位。在工程中，一般取长度、时间与质量（或力）的量度单位为基本单位，并用L、T、M（或F）来表示。在物理单位制中，L的量纲为m，T的量纲为s，M的量纲为kg。一切力学量的量度单位都可以从这些单位中导出来。显而易见，这种选取也不是任意的，例如我们已定义速度是位移与时间的比值，就不能同时选取速度、长度和时间作基本量，因为它们并非彼此独立的。

一个量的单位用基本单位来表达时，如果我们撇开基本单位的具体大小，而只限于基本单位的种类，如长度、时间和质量（或力）等，则我们说这个量具有长度几次、时间几次和质量几次（或力几次）的量纲。如此，任何特征量A的量纲为

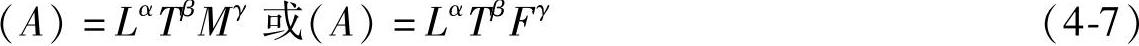(www.xing528.com)

在几何量中：α≠0，β=0，γ=0；运动量中：α≠0，β≠0，γ=0；动力量中：α、β、γ均不等于零，如：

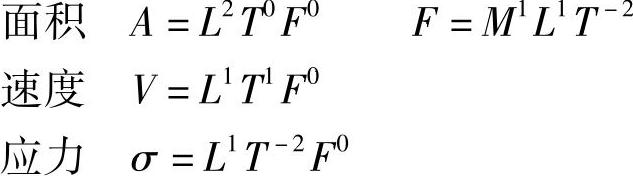
如A为无量纲的数，则（A）=1即α、β、γ皆等于零。有量纲的特征量的等式或不等式两边的量纲应该相同，这称为量纲齐次性原理。由此

事实上，在量度中不一定必须取L、T、M（或L、T、F）为基本单位，也可以取任意三个量纲独立的特征量a₁，a₂和a₃为基本单位，只要（a^x₁a^y_xa^z₃）=L⁰T⁰M⁰=1的解不存在（x、y和z同时为零的情况除外）。如此，任何特征量A的量纲均可表示为

根据量纲齐次性原理

式中，Π——量纲为一的数。

由此可见，假如描述某现象的特征量A，a₁，a₂，…，a_n之间有关系式

A=f（a₁，a₂，…，a_n）（4-9）

将其中三个量纲独立的特征量a₁，a₂和a₃取作基本量，那么其余n-3个特征量就可化成无量纲数（Π₁，Π₂，…，Π_n-3），即

如此，式（4-9）可写成

这就是量纲分析中的Π定理。它表明任何有量纲的量间的物理关系，必可化为无量纲数间的关系，从而减少了问题中的变量。这些无量纲数一般可以由理论计算或实验的方法来决定。这样，就可以从某一些已知特征量的数值，计算另一些特征量的数值。

（3）相似设计的方法 为了满足顾客的不同要求，工厂常设计和生产系列产品。所谓系列产品，是指具有相同功能、相同结构方案、相同或相似的加工工艺，且各产品的尺寸参数及性能指标具有一定的极差（公比）的产品。系列化产品的优越性在于：

1）不同规格的产品都是基于一种规格变化而形成的，可以有尽可能多的通用件。这就大大缩短了产品开发周期并节省成本，提高了产品的可靠性。

2）在满足顾客要求的前提下，系列产品遵循适当的参数变化规律，可以提高不同规格产品的生产批量，有利于稳定产品质量，降低成本。

3）对企业来说，系列产品便于库存管理；对顾客来说，系列产品的使用规则和方法相同，便于使用。

进行系列产品设计时，首先选定某一中档的产品为基型，对其进行最佳方案的设计，定出材料、参数和尺寸。然后，再按系列设计的原理，即通过相似原理，求出系列中其他产品的参数和尺寸。在产品系列设计中，一般采用几何相似产品系列设计和几何半相似产品系列设计。

（4）几何相似产品系列设计 这种设计方法的工作步骤为：

1）根据市场需求确定系列的尺寸范围和系列的分级数n。分级细可使系列产品的技术特性易于满足顾客的不同需求，具有较大的市场覆盖面；而分级粗则可使系列中每种规格有较大的批量，加工较为经济，降低成本。在设计之前，应对此进行权衡。

2）按产品功能要求，设计基型产品。基型产品的功能参数和尺寸应居于整个系列的中间位置。

3）根据相似关系，进行相似设计，求得系列中扩展产品每种规格的技术参数和几何尺寸。完全按几何级数相似设计的系列产品的各种参数和几何尺寸的级间比，具有一定的关系。

4）在计算扩展型产品技术参数和几何尺寸的同时，考虑到技术和工艺方面的种种限制，如铸件的壁厚、钻孔的直径和深度等，需要对某些尺寸进行适当的调整。

（5）几何半相似产品系列设计 在系列化设计时，以规格的产品的全部零件不一定都要按一种相似比变化，往往由于各种因素的影响，需要对相似比进行调整。这种具有不同级间比的相似系列，称为几何半相似系列。几何半相似产品系列设计应该按照工艺、使用要求等具体情况，来确定不同参数和尺寸的适当的比例关系。如车床系列设计中，中心高和最大回转直径D一般是成比例的，而车床中心距地面的距离、手柄尺寸等则可有所不同。